Circuncentro de un triángulo

Es decir, el circuncentro es el punto central de la circunferencia que contiene al triángulo en cuestión.

Otro concepto importante a detallar es que la mediatriz es aquella recta que, siendo perpendicular a uno de los lados del triángulo, divide dicho segmento en dos partes iguales.

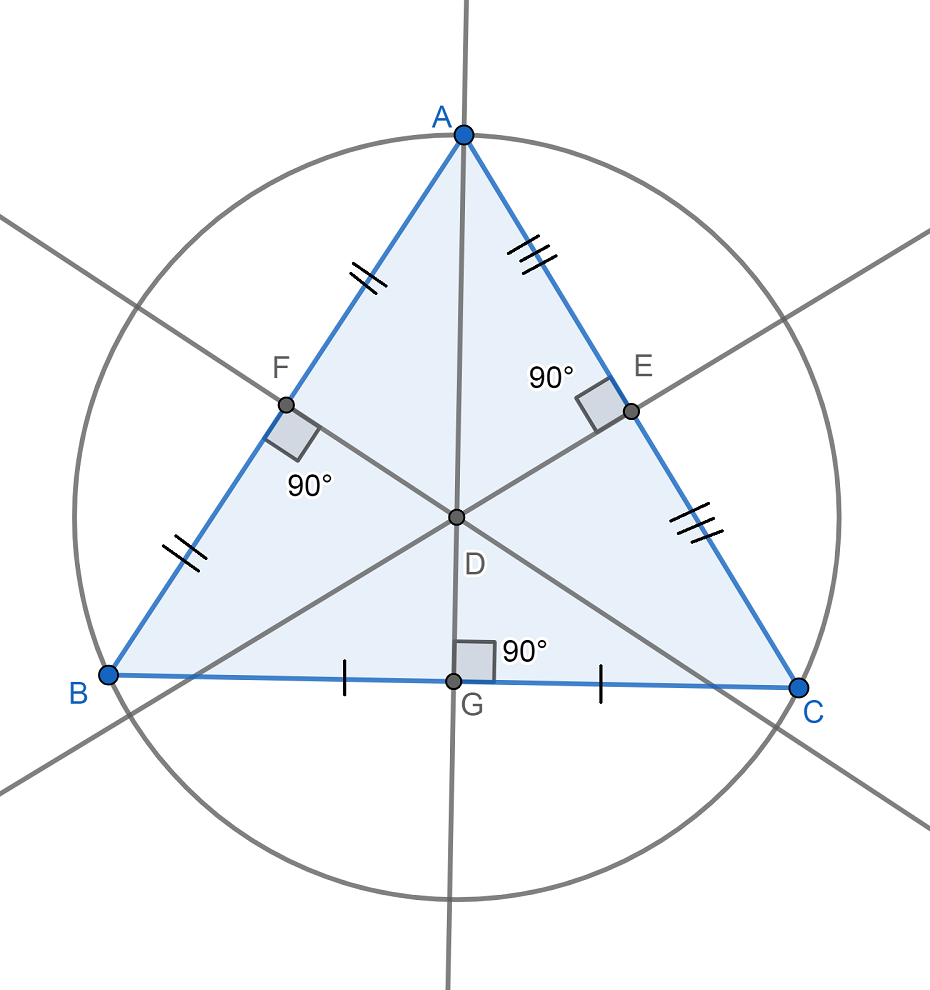
En la figura de arriba, por ejemplo, el punto D es el circuncentro de la figura. Asimismo, F, G y E son los puntos medios de cada lado con lo que se cumple que:

AE=EC, BF=FA, BG=GC

Una propiedad importante del circuncentro es que es equidistante a los tres vértices del triángulo, es decir, su distancia es la misma respecto a cada uno de sus vértices.

Cabe mencionar además que el circuncentro se encuentra alineado con el baricentro (punto de intersección de las medianas) y el ortocentro (punto de intersección de las alturas) del triángulo en la recta de Euler.

El circuncentro tiene ciertas características de acuerdo a qué tipo de triángulo estamos estudiando:

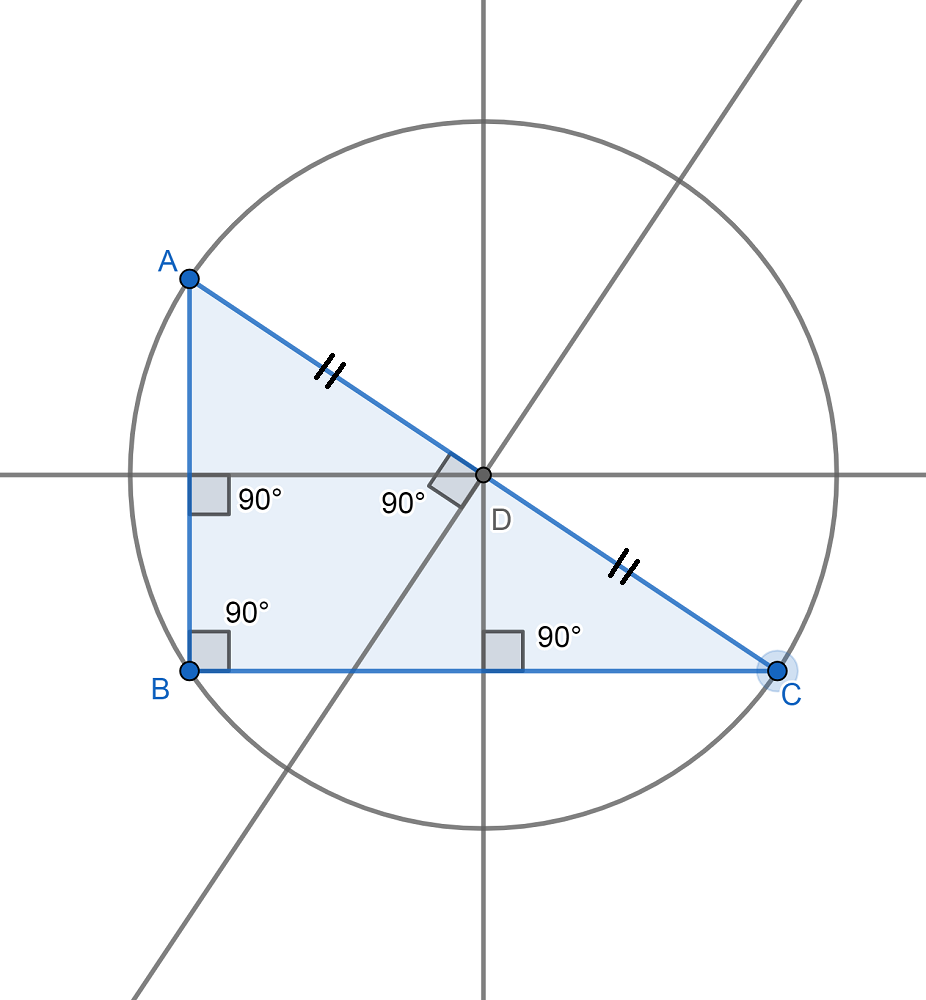
• Triángulo rectángulo: El circuncentro es el punto medio de la hipotenusa que es el segmento que se encuentra frente al ángulo recto interno de la figura.

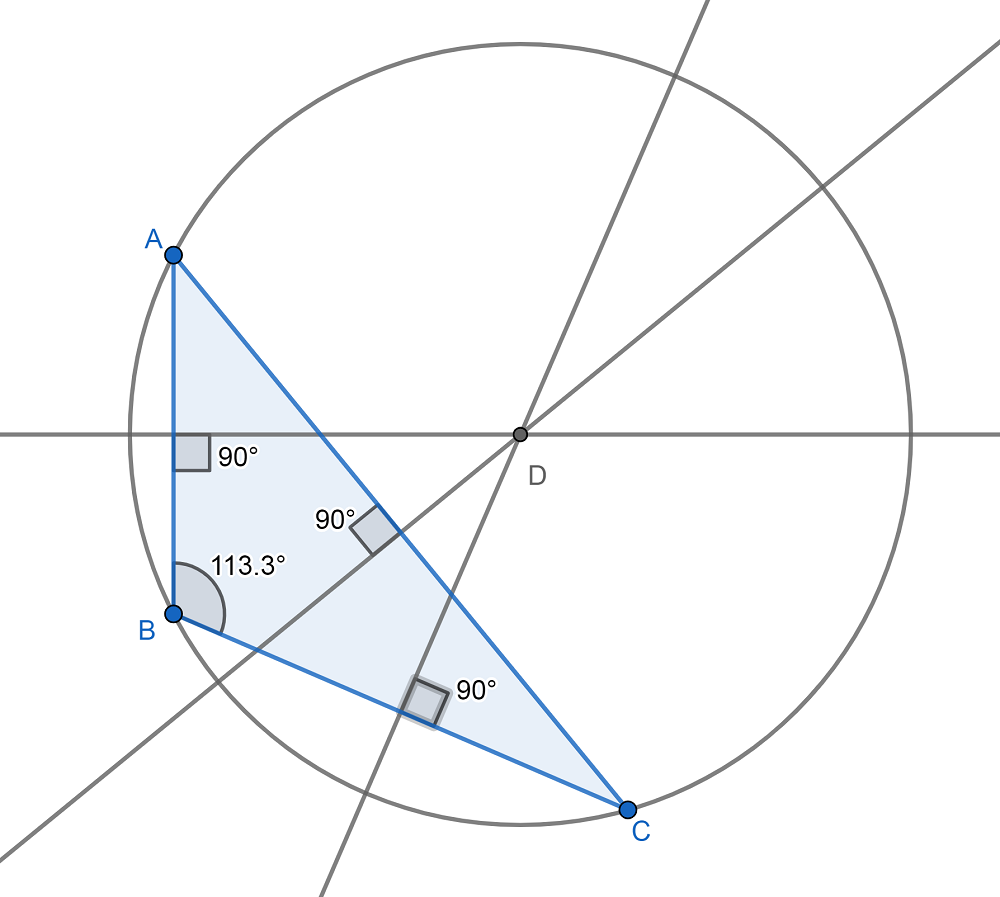
• Triángulo obtusángulo: En el caso de un triángulo obtusángulo (que tiene un ángulo obtuso o mayor de 90º) el circuncentro es exterior al triángulo.

• Triángulo acutángulo: En el caso de un triángulo acutángulo (donde los tres ángulos interiores son menores a 90º), el circuncentro se encuentra dentro de la figura, como observamos en la primera imagen de este artículo.

Supongamos que tenemos la información de la ecuación de dos de las rectas que son mediatrices del triángulo:

y=0,8x+4,4

y=-0,6x+7,6

¿Cuál será su circuncentro? Lo que debemos hacer es hallar cuál será el punto en el que los valores de x e y coincidirán en las dos ecuaciones:

0,8x+4,4=-0,6x+7,6

1,4x=3,2

x=2,2857

Luego despejo y:

y= (2,2857 x 0,8) + 4,4 = 6,2286

Por lo tanto, el circuncentro se encontrará en el siguiente punto del plano cartesiano: (2,2857;6,2286).