Rectas perpendiculares
Las rectas perpendiculares son aquellas que al cruzarse forman cuatro ángulos iguales, siendo cada uno un ángulo recto, es decir, que mide 90º.
Visto de otro modo, al intersecarse dos rectas perperndiculres, un ángulo completo o perigonal queda dividido en cuatro partes idénticas entre sí.
Las rectas perpendiculares son un posibilidad entre los casos de rectas secantes. Estas son aquellas que se cruzan o, para explicarlo de otra forma, tienen un punto en común.
Vale recodar que un recta es una secuencia indefinida que va en una sola dirección, es decir, no presenta curvas, y no tiene ni un inicio ni un final.
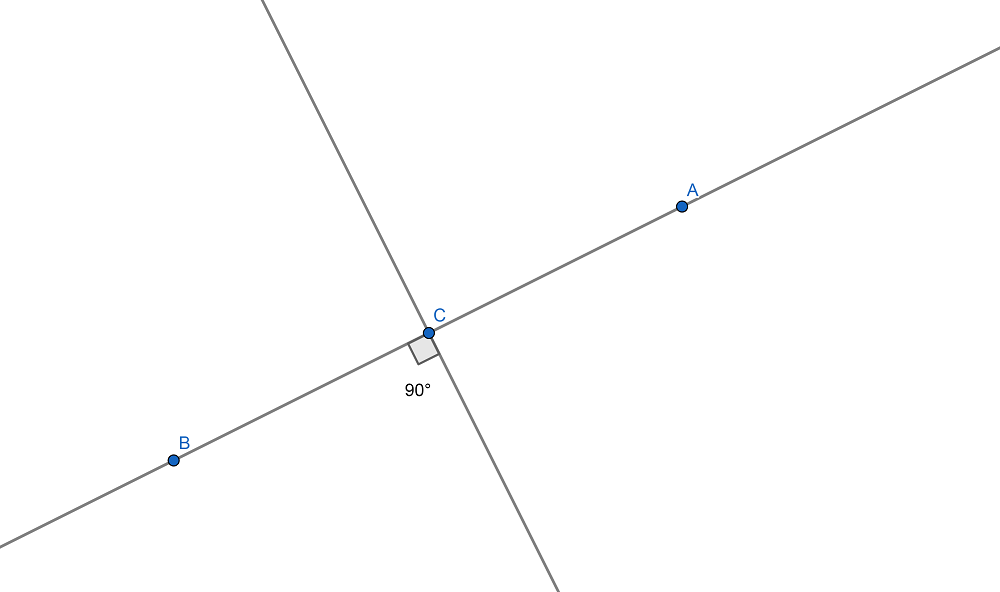
Ecuación de las rectas perpendiculares
Si la recta 1 y la recta 2 son perpendiculares, la pendiente de una es igual al inverso de la pendiente de la otra y con el signo cambiado de positivo a negativo o viceversa. Es decir, si en la recta 1 la pendiente es, por ejemplo, 1/5, en la recta 2, la pendiente será -5. Visto de otro de modo, se cumple que:
m1=-1/m2
En la ecuación, m1 es la pendiente de la recta 1, mientras que m2 es la pendiente de la recta 2, siendo ambas perpendiculares.
Recordemos que, en la geometría analítica una recta se puede representar con una ecuación del siguiente tipo:
y=mx+b
Así, en la ecuación y es la coordenada en el eje de las ordenadas (vertical), x es la coordenada en el eje de las abscisas (horizontal), m es la pendiente (inclinación) que forma la recta respecto al eje de las abscisas, y b es el punto en el que la recta corta el eje de las ordenadas.
Podemos ver en la imagen inferior que la pendiente de una de las rectas es -2, y la de la otra, 0,5, que es lo mismo que 1/2. De ese modo, se cumple lo explicado líneas arriba.
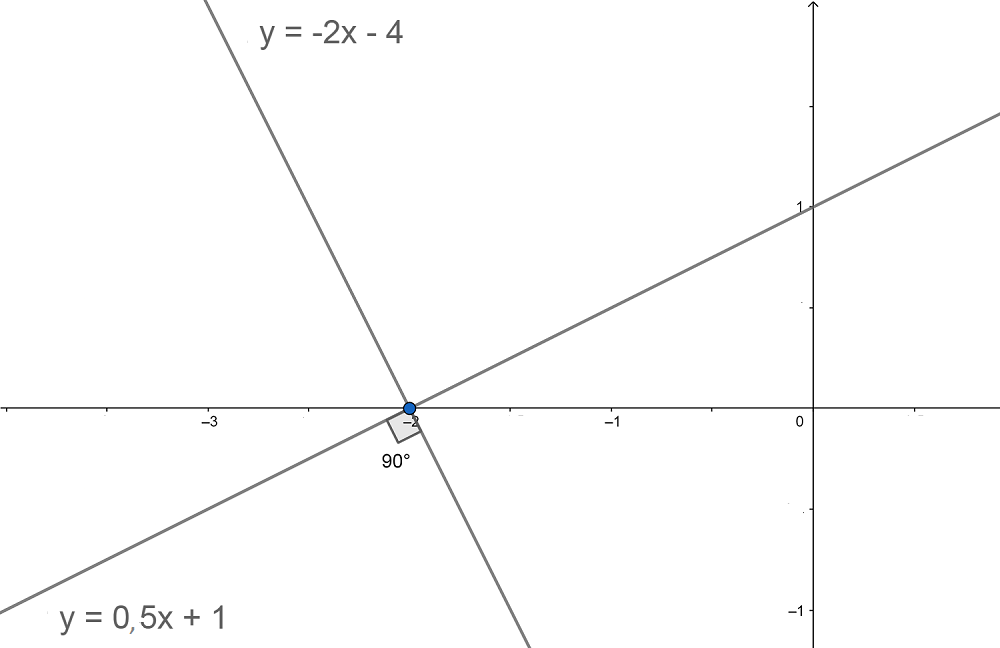
Ejemplo de rectas perpendiculares
Podemos determinar si dos rectas son perpendiculares sabiendo dos de sus puntos. Por ejemplo, supongamos que la recta 1 pasa por el punto A(0,5;4) y el punto B(0;2). En tanto, la recta 2 pasa por el punto C(2;2,5) y el punto D(-2;3,5). ¿Son la recta 1 y la recta 2 perpendiculares?
Primero, hallamos la pendiente de la recta 1, dividiendo la variación en el eje y entre la variación en el eje y cuando pasamos del punto A al punto B. Así, en el eje y pasamos de 4 a 2, variando en -2. En tanto, en el eje x, pasamos de 0,5 a 0, variando en -0,5. Por lo tanto, siendo m1 la pendiente de la recta 1:
m1=(2-4)/(0-0,5)=-2/-0,5=4
Luego, hallamos pendiente de la recta 2 (m2). Procedemos de la misma forma, pero pasando del punto C al punto D.
m2=(3,5-2,5)/(-2-2)=1/(-4)=-1/4=-0,25
Como vemos, m1=-1/m2 dado que 4=-(1/-0,25). Por lo tanto, la recta 1 y la recta 2 son perpendiculares.
