Triángulo

El triángulo es una figura geométrica muy importante y base de otros polígonos. Así, cualquier polígono con más de tres lados (como el cuadrado) puede dividirse en distintos triángulos cuando se trazan sus diagonales, como vemos en la figura de abajo.

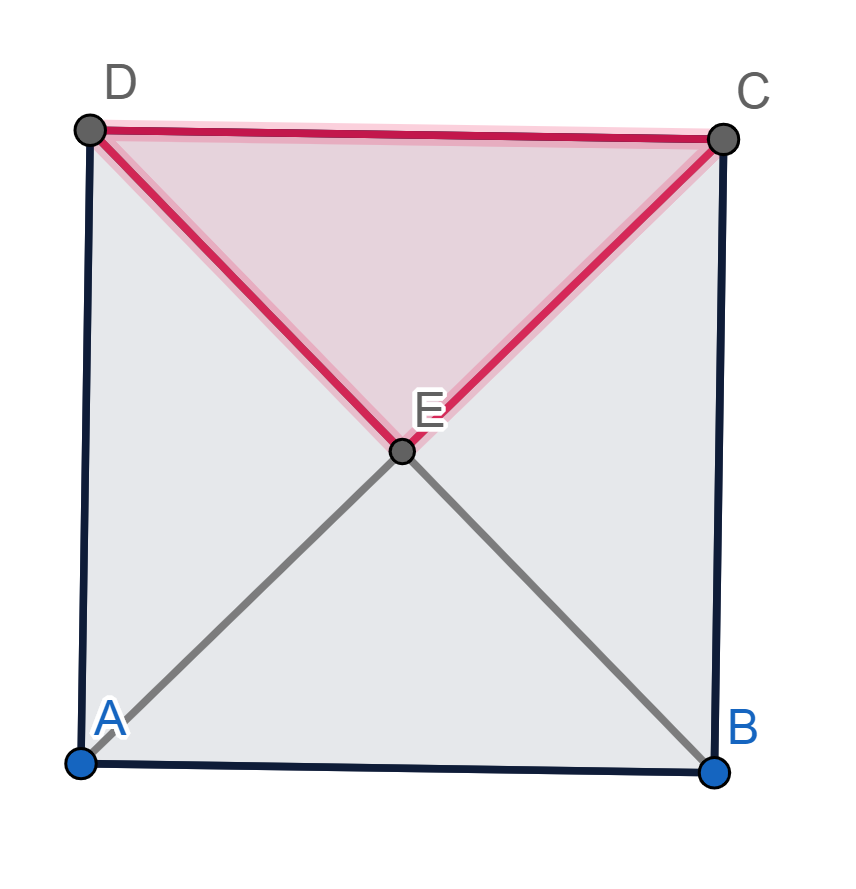
Vale recordar que la diagonal es aquel segmento que une un vértice de la figura geométrica con el vértice del lado opuesto.

Cabe señalar además que un polígono es una figura geométrica bidimensional que se forma de la unión de distintos puntos (que no formen parte de la misma línea) mediante segmentos de recta.

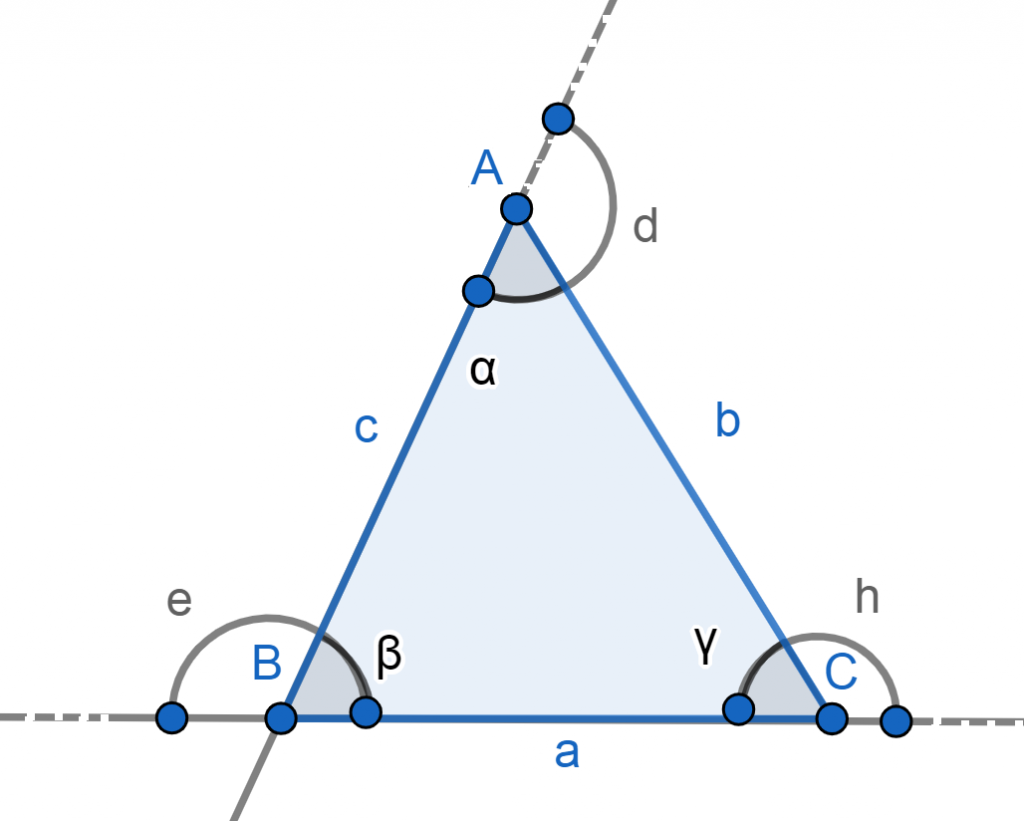
Tomando como referencia la figura de abajo, los elementos del triángulo son los siguientes:

• Vértices: A, B, C.
• Lados: AB, BC, AC.
• Ángulos interiores: ∝, β, γ.
• Ángulos exteriores: e, d, h. Cada uno es suplementario al ángulo interior del mismo lado. Es decir, se cumple que:

180º= ∝+d= β+e= h+γ

Asimismo, una propiedad importante del triángulo es que sus ángulos interiores suman 180º, es decir:

∝+β+γ= 180º

Basándonos en la figura de la parte inferior, para hallar el perímetro y área de un triángulo, podemos utilizar las siguientes fórmulas:

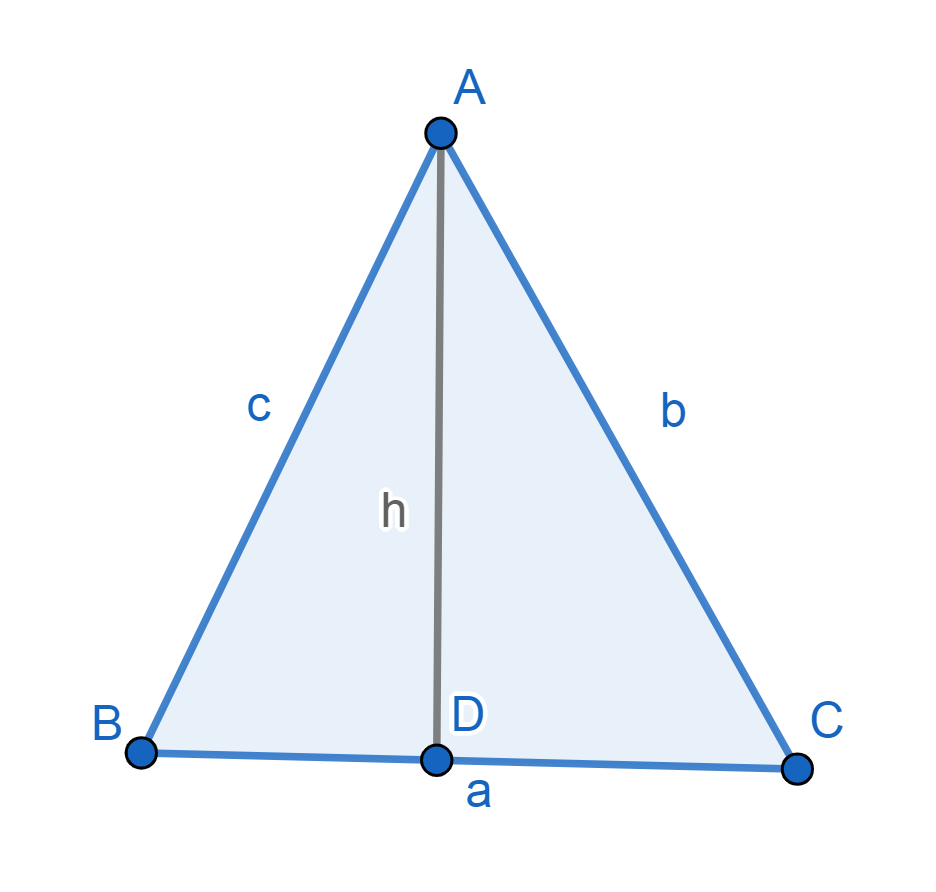
• Perímetro: Es simplemente la suma de los lados: a + b + c
• Área: Para hallar el área de un triángulo se requiere multiplicar la longitud de una base (uno de los lados), por su altura, y dividirlo entre 2. Por ejemplo, en la figura de arriba podríamos multiplicar (a*h)/2. Sin embargo, puede ser que no siempre nos den como información el valor de h. En ese caso, podemos aplicar la fórmula de Herón, donde A es el área y s, el semiperímetro, es decir, el perímetro entre dos (s=P/2):

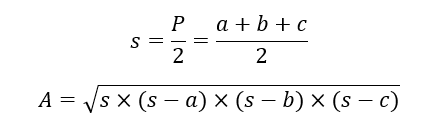
Debemos acotar que, en el caso de un triángulo rectángulo, de los lados que forman el ángulo recto, uno es la base y el otro es la altura, por lo que es más fácil calcular el área.

Supongamos que tenemos un triángulo con tres lados, que miden 13, 10 y 7 metros. ¿Cuál sería su perímetro y su área?

Ahora, supongamos que tenemos el caso de un triángulo rectángulo y sabemos que los lados que forman el ángulo recto miden 10 y 7 metros. Entonces, obtenemos el área de una forma simple:

A = (10*7) / 2 = 35 m²

Los dos resultados no coinciden exactamente porque un triángulo rectángulo debe cumplir el teorema de Pitágoras. Es decir, los lados que forman el ángulo recto, que son los catetos, al ser elevados al cuadrado y sumarse, deben dar igual a la longitud del tercer lado, llamado hipotenusa (x), elevada al cuadrado, como vemos a continuación:

7² + 10² = x²

49 + 100 = x²

149 = x²

x = 12,2066 m

Es decir, para que el triángulo sea rectángulo, sus lados no pueden medir 10,7 y 13 metros, sino 10,7 y 12,2066 metros.