Vértice
El vértice es el punto de una figura geométrica donde se unen dos o más elementos unidimensionales. Estos pueden ser curvas, vectores, rectas, semirrectas o segmentos.
En este punto, debemos definir los siguientes conceptos:
- Curva: Es aquella línea no recta.
- Vector: Son representaciones gráficas de una magnitud y se dibujan como flechas.
- Recta: Es una línea conformada por una cantidad infinita de puntos que va en una sola dirección.
- Semirrecta: Es cada una de las dos porciones en las que queda dividida una recta al ser partida desde cualquiera de los puntos que la componen.
- Segmento: Es la porción de una recta que, a diferencia de una semirrecta, está limitada por dos puntos o extremos, y no solo por el punto de división.
Los vértices forman parte de la construcción de un polígono (figura bidimensional) o de un poliedro (figura tridimensional).
Otra forma de explicarlo es que los vértices son las esquinas de las figuras geométricas, y desde donde se forman los ángulos de las mismas.
Vértice de un polígono
En el caso de un polígono, el vértice es el punto donde se unen dos de sus lados, y al cual se corresponde un ángulo interior, así como uno exterior.
Cabe señalar que el número de vértices de un polígono es igual al número de lados. Por ejemplo, en el caso de un cuadrado tenemos cuatro vértices, mientras que en un hexágono tenemos seis.
Por ejemplo, en la imagen inferior, los vértices cuadrado son A, B, C y D.
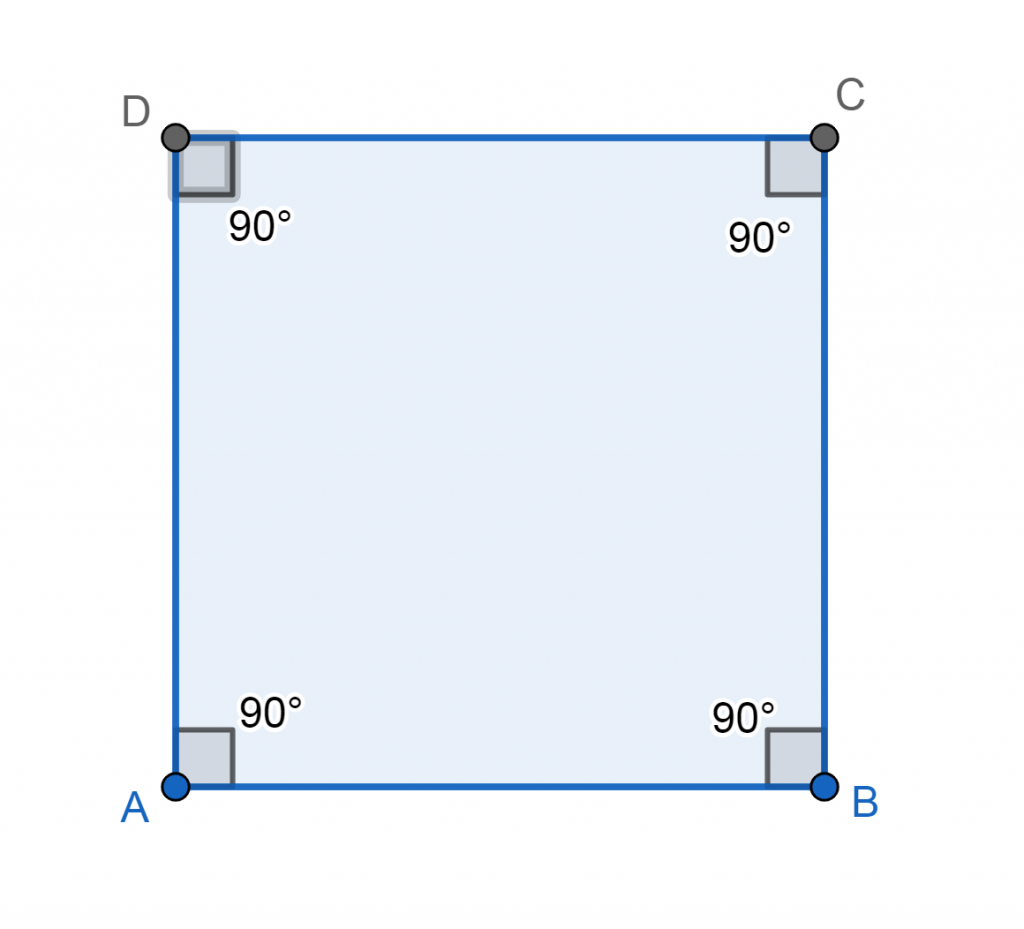
Cabe mencionar que en el caso de un polígono cóncavo tenemos dos tipos de vértice:
- Oreja: Si la diagonal que une los vértices vecinos se encuentra dentro de la figura. Su respectivo ángulo interior es agudo. Es decir, mide menos que 90º. En la imagen inferior, los vértices A, B y C son orejas porque la diagonal que une B y F (vértices vecinos de A), aquella que une A y C (vértices vecinos de B), y la diagonal que une B y D (vértices vecinos de C), todos se encuentran dentro de la figura.
- Boca: Si la diagonal que une los vértices vecinos se ubica fuera del polígono. Su ángulo interior siempre es obtuso. Es decir, mide más que 90º, pero menos que 180º. En el gráfico inferior, D es una boca porque el vértice que une C y E se encuentra totalmente fuera de la figura. Igualmente, el vértice F es otra boca porque la diagonal AE se encuentra fuera del polígono.
Vale señalar además que pueden existir vértices que no se encuentran en ninguna de las categorías señaladas porque pasan tanto por fuera como por dentro del polígono. Un ejemplo es el vértice E en la imagen inferior, pues la diagonal CF tiene una parte fuera y otra dentro de la figura.
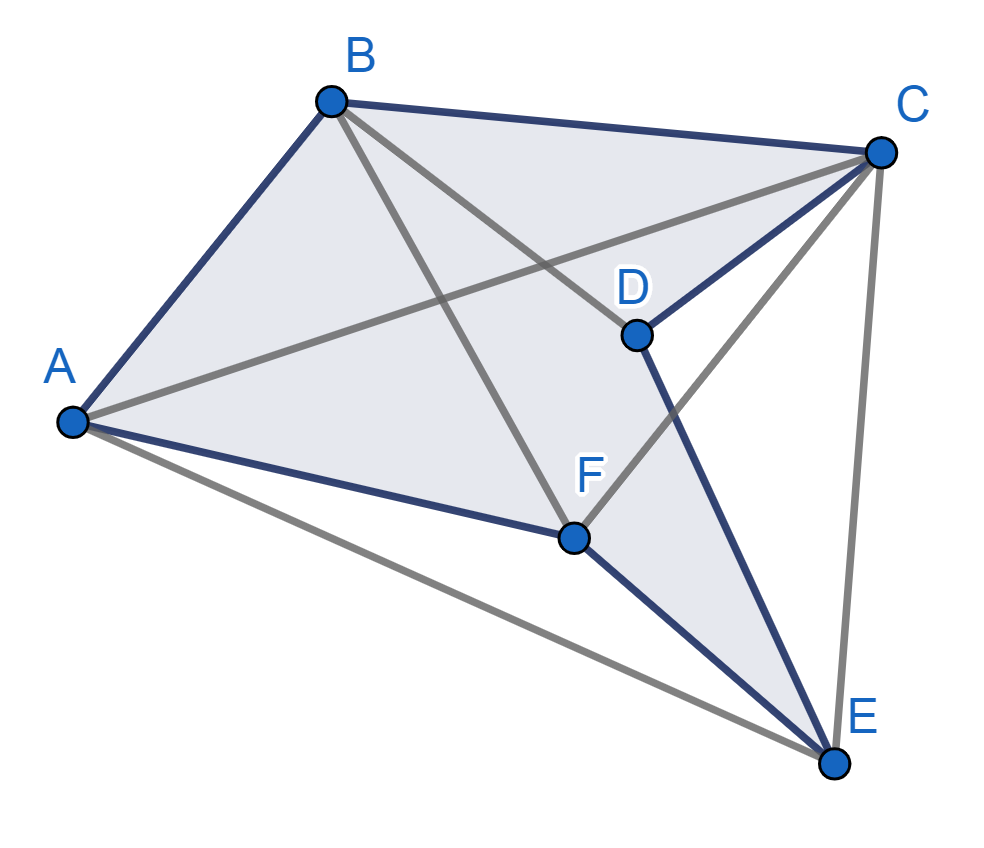
Cabe recordar una diagonal es aquel segmento que une dos vértices opuestos de una figura.
Un hecho importante además es que todo polígono cóncavo tiene al menos un vértice tipo boca y dos vértices tipo oreja.
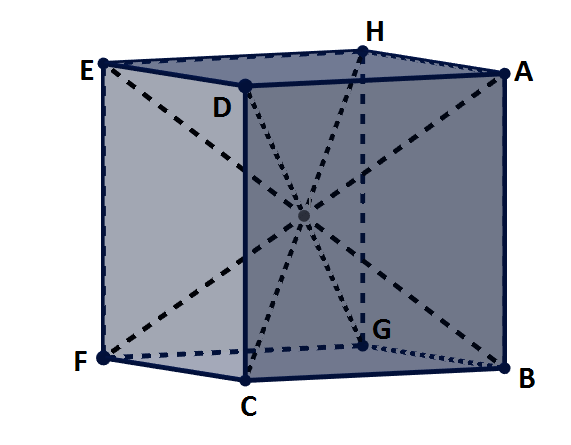
Vértice de un poliedro
En un poliedro, los vértices son los puntos donde se observa la intersección de las aristas, uniéndose así tres o más caras de la figura.
Otra forma de definir los vértices del poliedro sería como los puntos extremos de cada arista. Además, recordemos que las aristas son los segmentos que unen dos caras de la figura.
En la imagen de abajo, que es un cubo o hexaedro regular, los vértices son A, B, C, D, E, F, G y H