Triángulo acutángulo
El triángulo acutángulo es aquel cuyos tres ángulos interiores son agudos, es decir, miden menos que 90º.
Esta categoría de triángulo es un caso muy particular dentro de los tipos de triángulo según la medida de sus ángulos internos.
En este punto, vale recordar que el triángulo es un polígono, es decir, una figura geométrica bidimensional que se constituye de la unión de distintos puntos (que no formen parte de la misma línea) mediante segmentos de recta. De ese modo, se construye un espacio cerrado.
Elementos del triángulo acutángulo
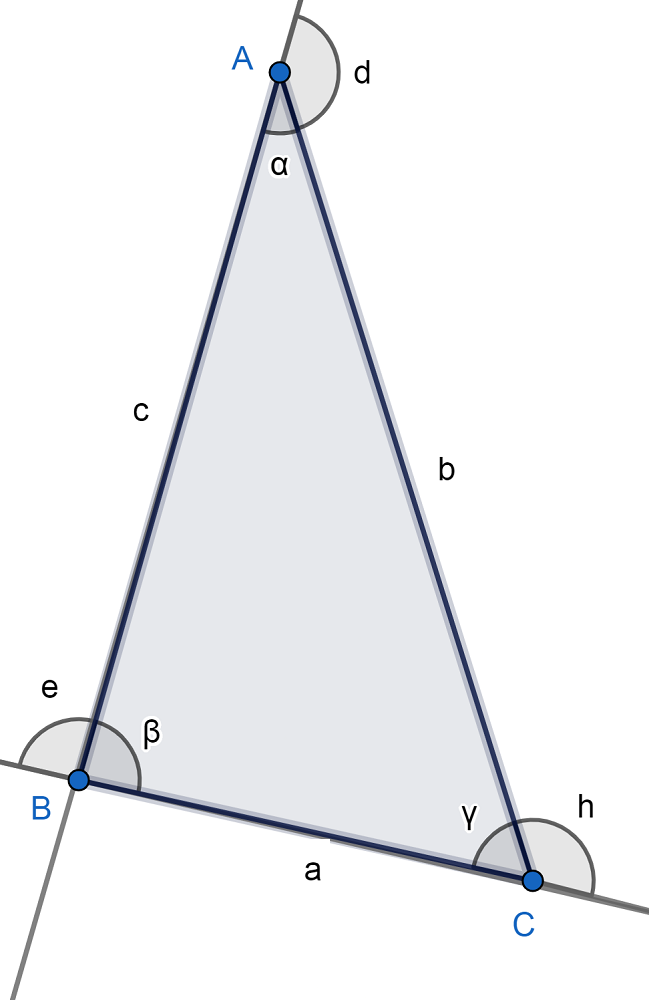
Guiándonos de la figura de abajo, los elementos del triángulo acutángulo son los siguientes:
- Vértices: A, B, C.
- Lados: AB, BC, AC.
- Ángulos interiores: ∝, β, γ. Todos suman 180º.
- Ángulos exteriores: e, d, h. Cada uno es suplementario al ángulo interior del mismo lado. Es decir, se cumple que: 180º= ∝+d= β+e= h+γ. Lo anterior quiere decir que todos los ángulos exteriores son obtusos (mayores que 90º).
Tipos de triángulo acutángulo
Los tipos de triángulo acutángulo, según la medida de sus lados, son los siguientes:
- Equilátero: Todos sus lados miden igual y sus ángulos interiores también son iguales y miden 60º. Las tres alturas, respecto a los tres lados, son ejes de simetría. Esto significa que dividen a la figura en dos triángulos iguales.
- Isósceles: Dos de sus lados miden lo mismo y el otro es distinto.
- Escaleno: Todos sus lados y ángulos interiores son diferentes.
Perímetro y área del triángulo acutángulo
Las características del triángulo acutángulo se pueden medir en base a las siguientes fórmulas:
- Perímetro(P): Es la suma de los lados que, según la figura de arriba donde señalamos los elementos, sería: P=a+b+c
- Área(A): En este caso, nos basamos en la fórmula de Herón donde s es el semiperímetro, es decir, P/2.
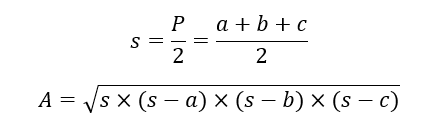
Ejemplo de triángulo acutángulo
Supongamos que tenemos un triángulo con dos ángulos interiores que miden 40º. ¿Puede tratarse de un triángulo acutángulo? Recordemos que los tres ángulos internos deben sumar 180º. Por lo tanto, siendo x el ángulo desconocido:
40º+40º+x=180º
80º+x=180º
x=100º
Por lo tanto, x es un ángulo obtuso porque mide más de 90º. Lo que quiere decir que el triángulo no es acutángulo, sino obtusángulo.
Ahora, veamos otro ejercicio. Observemos la siguiente figura:
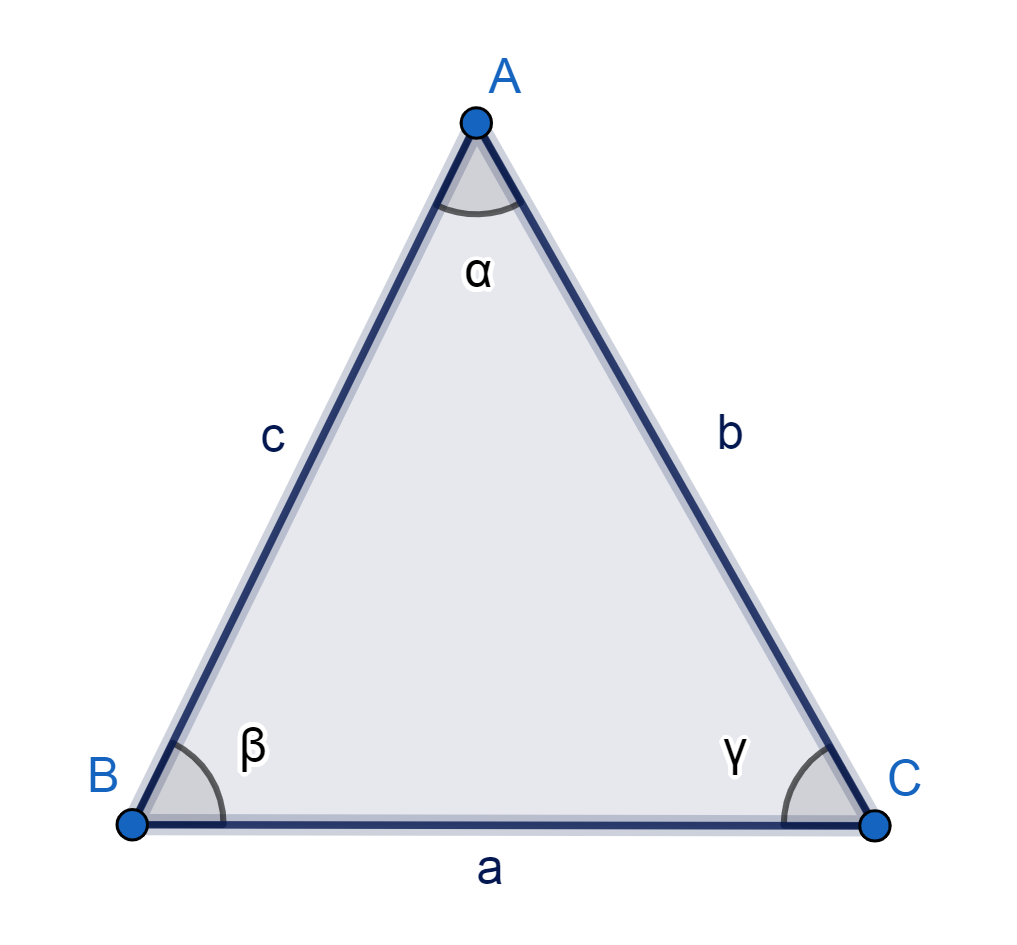
Supongamos que el lado BC(a) mide 12 metros. α mide 55º, y β mide 65º. ¿Cuál es el perímetro y área de la figura?
Primero, nos basaremos en el teorema del seno, dividiendo la longitud de cada lado entre el seno de su ángulo opuesto:
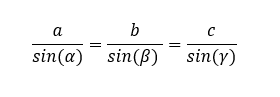
Además, si α+β+γ=180, entonces:
55 + 65 + γ = 180
120 + γ =180
γ = 60
Por lo tanto, es un caso de triángulo acutángulo.
Despejamos b:
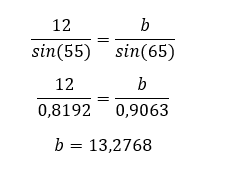
Despejamos c:
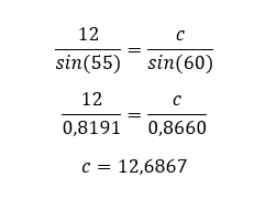
Calculamos el perímetro y el semiperímetro:
P = 12 + 13,2768 + 12,6867 = 37,9634 metros
S = P/2 = 18,9817 metros
Finalmente, calculamos el área con la fórmula presentada previamente:
