Modelo atómico de Bohr: características, postulados, limitaciones
El modelo atómico de Bohr es la concepción del físico danés Niels Bohr (1885-1962) acerca de la estructura del átomo, publicada en 1913. En el átomo de Bohr, los electrones alrededor del núcleo ocupan únicamente ciertas órbitas permitidas, gracias a una restricción llamada cuantización.
Para Bohr, la imagen del átomo como un sistema solar en miniatura, con los electrones orbitando alrededor del núcleo, no era del todo consistente con el hecho de que las cargas eléctricas, cuando son aceleradas, irradian energía.

Un átomo así no sería estable, pues terminaría por colapsar tarde o temprano debido a que los electrones se precipitarían en espiral hacia el núcleo. Y para ese entonces, hacía ya 50 años que se conocían los patrones de luz característicos que emiten el hidrógeno y otros gases al calentarse.
El patrón o espectro consiste en una serie de líneas brillantes de ciertas longitudes de onda muy específicas. Y el átomo de hidrógeno no colapsa por emitir luz.
Para explicar por qué el átomo es estable pese a ser capaz de irradiar energía electromagnética, Bohr propuso que el momentum angular solamente podía adoptar determinados valores, y por ende la energía también. Esto es lo que se entiende por cuantización.
Aceptando que la energía estaba cuantizada, el electrón tendría la estabilidad necesaria para no precipitarse hacia el núcleo destruyendo al átomo.
Y el átomo únicamente irradia energía luminosa cuando el electrón efectúa transiciones de una órbita a otra, siempre en cantidades discretas. De esta forma queda explicada la presencia de patrones de emisión en el hidrógeno.
Bohr compuso de esta manera una visión del átomo integrando conceptos conocidos de la mecánica clásica con los recién descubiertos, tales como la constante de Planck, el fotón, el electrón, el núcleo atómico (Rutherford había sido mentor de Bohr) y los mencionados espectros de emisión.
Índice del artículo
- 1 Características principales del modelo de Bohr
- 2 Postulados del modelo atómico de Bohr
- 3 Limitaciones
- 4 Artículos de interés
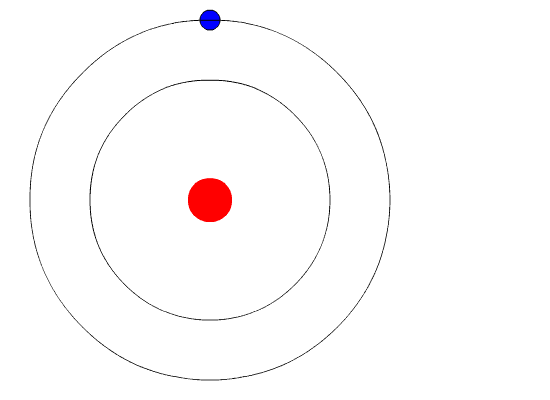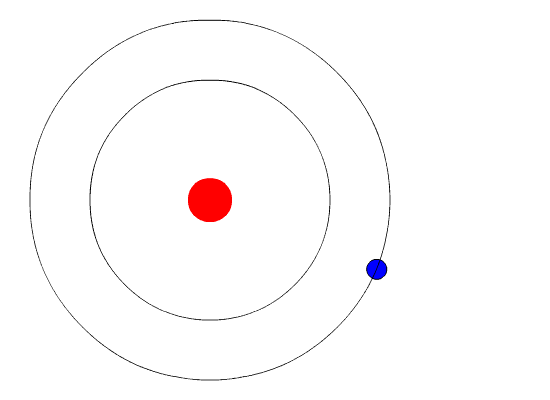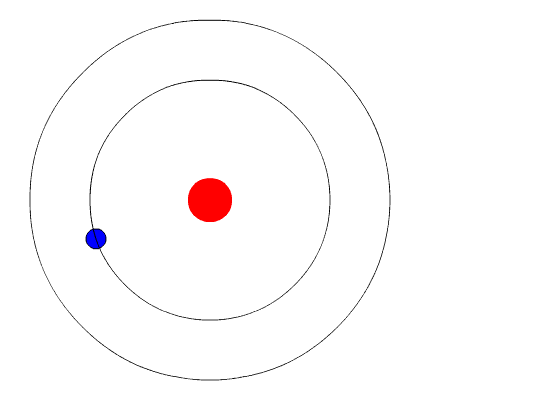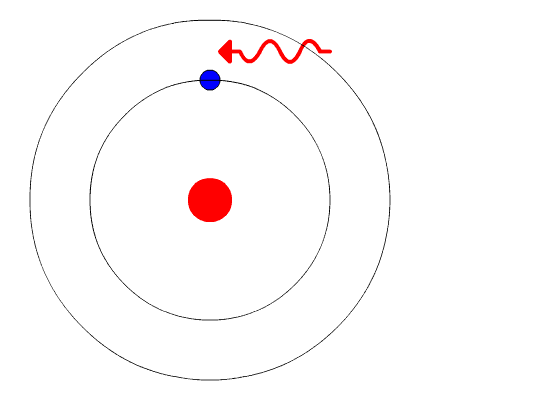
El modelo atómico de Bohr supone que el electrón se mueve en una órbita circular alrededor del núcleo por acción de la fuerza de atracción electrostática de Coulomb y propone que el momentum angular del electrón está cuantizado.
Veamos cómo integrar ambos conceptos en forma matemática:
Sea L la magnitud del momentum angular, m la masa del electrón, v la rapidez del electrón y r el radio de la órbita. Para calcular L tenemos:
L = m⋅r⋅v
Bohr propuso que L era igual a múltiplos enteros de la constante h/2π, donde h es la constante de Planck, introducida poco tiempo atrás por el físico Max Planck (1858-1947) al resolver el problema de la energía emitida por un cuerpo negro, un objeto teórico que absorbe toda la luz incidente.
Su valor es h = 6.626 × 10−34 J・s, mientras que a h/2π se denota como ħ, que se lee “h barra”.
Por lo tanto, el momentum angular L queda:
m⋅r⋅v = nħ, con n = 1,2 ,3…
Y de esta condición se deducen los radios de las órbitas permitidas para el electrón, como veremos seguidamente.
En lo que sigue supondremos el más simple de los átomos: el de hidrógeno, el cual consta de un solo protón y un electrón, ambos con carga de magnitud e.
La fuerza centrípeta que mantiene al electrón en su órbita circular es proporcionada por la atracción electrostática, cuya magnitud F es:
F = ke2/r2
Donde k es la constante electrostática de la ley de Coulomb y r la distancia electrón-protón. Sabiendo que en un movimiento circular la aceleración centrípeta ac viene dada por la razón entre el cuadrado de la rapidez y la distancia r:
ac = v2 / r
Por segunda ley de Newton, la fuerza neta es el producto de la masa m por la aceleración:
mv2/r = ke2/r2
Simplificando el radio r se obtiene:
m⋅v2r = ke2
Combinando esta expresión con la del momentum angular tenemos un sistema de ecuaciones, dado por:
1) mv2r = ke2
2) r = n ħ/mv
La idea es resolver el sistema y determinar r, el radio de la órbita permitida. Un poco de álgebra elemental conduce a la respuesta:
r = (nħ)2 / k⋅m⋅e2
Con n = 1, 2, 3, 4, 5…
Para n = 1 tenemos el menor de los radios, llamado radio de Bohr ao con un valor de 0,529 × 10−10 m. Los radios de las demás órbitas se expresan en términos de ao.
De esta manera Bohr introduce el número cuántico principal n, señalando que los radios permitidos están en función de la constante de Planck, la constante electrostática y la masa y carga del electrón.

Bohr combina hábilmente la mecánica newtoniana con los nuevos descubrimientos que se venían dando en forma continua durante la segunda mitad del siglo XIX y comienzos del siglo XX. Entre ellos el revolucionario concepto del “cuanto”, del cual el mismo Planck afirmó no estar muy convencido.
Mediante su teoría, Bohr pudo explicar satisfactoriamente las series del espectro del hidrógeno y predecir emisiones de energía en el rango del ultravioleta y el infrarrojo, mismas que aún no habían sido observadas.
Podemos resumir sus postulados de la siguiente manera:
El electrón gira alrededor del núcleo en órbita circular estable, con movimiento circular uniforme. El movimiento se debe a la atracción electrostática que el núcleo ejerce sobre él.
El momento angular del electrón está cuantizado de acuerdo a la expresión:
L = mvr = nħ
Donde n es un número entero: n = 1, 2, 3, 4…, lo cual lleva a que el electrón solamente puede estar en ciertas órbitas definidas, cuyos radios son:
r = (n ħ)2 / k m e2
Dado que el momento angular está cuantizado, la energía E también. Se puede demostrar que E viene dada por:
El electrón voltio o eV, es otra unidad para la energía, muy utilizada en física atómica. El signo negativo en la energía asegura la estabilidad de la órbita, indicando que habría que hacer trabajo para separar al electrón de esta posición.
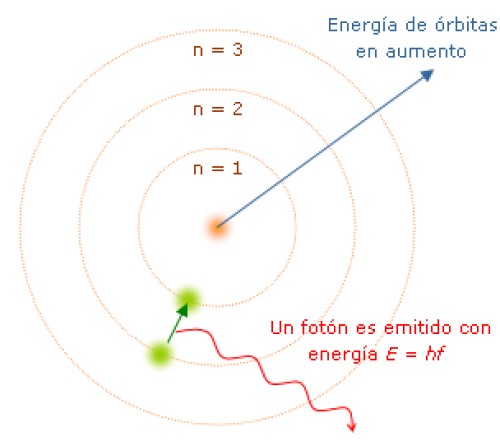
Mientras el electrón está en su órbita no absorbe ni emite luz. Pero cuando salta de una órbita de mayor energía a una inferior sí lo hace.
La frecuencia f de la luz emitida depende de la diferencia entre los niveles de energía de las órbitas:
E = hf = Einicial − Efinal
El modelo de Bohr tiene ciertas limitaciones:
-Únicamente se aplica con éxito al átomo de hidrógeno. Los intentos por aplicarlo a átomos más complejos no dieron resultado.
-No responde por qué algunas órbitas son estables y otras no. El hecho de que la energía en el átomo estuviera cuantizada funcionaba muy bien, pero el modelo no proporcionaba una razón, y eso era algo que causaba incomodidad a los científicos.
-Otra limitación importante es que no explicaba las líneas adicionales emitidas por los átomos en presencia de campos electromagnéticos (efecto Zeeman y efecto Stark). O por qué algunas líneas del espectro eran más intensas que otras.
-El modelo de Bohr tampoco considera efectos relativistas, los cuales es necesario tomar en cuenta, puesto que experimentalmente se determinó que los electrones son capaces de alcanzar velocidades bastante cercanas a la de la luz en el vacío.
-Da por sentado que es posible conocer con precisión la posición y la velocidad del electrón, pero lo que en verdad se calcula es la probabilidad de que el electrón ocupa una determinada posición.
Pese a sus limitaciones, el modelo tuvo un gran éxito en su momento, no solamente por integrar nuevos descubrimientos con elementos ya conocidos, sino porque puso de manifiesto nuevas interrogantes, dejando claro que el camino hacia una explicación satisfactoria del átomo estaba en la mecánica cuántica.
Modelo atómico de Schrödinger.
