Modelo atómico de Dirac Jordan: características y postulados
El modelo atómico de Dirac-Jordan es la generalización relativista del operador hamiltoniano en la ecuación que describe la función de onda cuántica del electrón. A diferencia del modelo precedente, el de Schrodinger, no es necesario imponer el espín mediante el principio de exclusión de Pauli, ya que aparece de forma natural.
Además, el modelo de Dirac-Jordan incorpora las correcciones relativistas, la interacción espín-órbita y el término de Darwin, que dan cuenta de la estructura fina de los niveles electrónicos del átomo.
A partir de 1928, los científicos Paul A. M. Dirac (1902-1984) y Pascual Jordan (1902-1980), se propusieron generalizar la mecánica cuántica desarrollada por Schrodinger, para que incluyese las correcciones de la relatividad especial de Einstein.
Dirac parte de la ecuación de Schrodinger, que consta de un operador diferencial, llamado hamiltoniano, que opera sobre una función conocida como la función de onda del electrón. Sin embargo Schrodinger no tomó en cuenta los efectos relativistas.
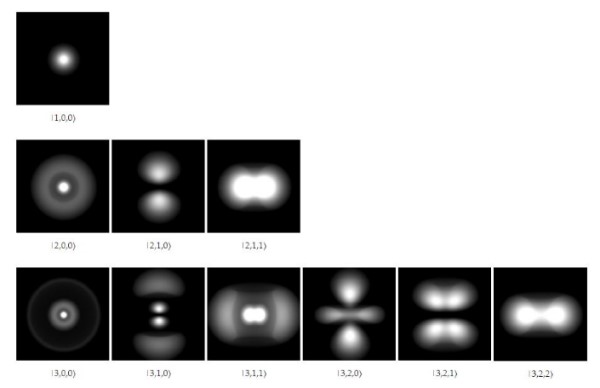
Las soluciones de la función de onda permiten calcular las regiones donde con cierto grado de probabilidad se encontrará el electrón alrededor del núcleo. Estas regiones o zonas se llaman orbitales y dependen de ciertos números cuánticos discretos, que definen la energía y el momentum angular del electrón.
Índice del artículo
En las teorías mecánico cuánticas, ya sean relativistas o no, no existe el concepto de órbitas, ya que ni la posición ni la velocidad del electrón pueden precisarse simultáneamente. Y además, precisar una de las variables conduce a una imprecisión total en la otra.
Por su parte, el hamiltoniano es un operador matemático que actúa sobre la función de onda cuántica y se construye a partir de la energía del electrón. Por ejemplo, un electrón libre tiene energía total E que depende de su momentum lineal p de esta forma:
E = (p2)/ 2m
Para construir el hamiltoniano se parte de esta expresión y se sustituye p por el operador cuántico para el momentum:
p = -i ħ ∂ /∂r
Es importante destacar que los términos p y p son diferentes, ya que el primero es el momentum y el otro es el operador diferencial asociado al momentum.
Adicionalmente, i es la unidad imaginaria y ħ la constante de Planck dividida entre 2π, de esta manera se obtiene el operador hamiltoniano H del electrón libre:
H = (ħ2/2m) ∂2 /∂r2
Para encontrar el hamiltoniano del electrón en el átomo, se añade la interacción del electrón con el núcleo:
H = (ħ2/2m) ∂2 /∂r2 – eΦ(r)
En la expresión anterior -e es la carga eléctrica del electrón y Φ(r) el potencial electrostático producido por el núcleo central.
Ahora, el operador H actúa sobre la función de onda ψ de acuerdo a la ecuación de Schrodinger, que se escribe así:
H ψ = (i ħ ∂ /∂t) ψ
Primer postulado: la ecuación de onda relativista tiene la misma estructura que la ecuación de onda de Schrodinger, lo que cambia es el H:
H ψ = (i ħ ∂ /∂t) ψ
Segundo postulado: el operador hamiltoniano se construye partiendo de la relación energía-momentum de Einstein, la cual se escribe así:
E = (m2 c4 + p2 c2)1/2
En la relación anterior, si la partícula tiene momentum p = 0 entonces se tiene la famosa ecuación E = mc2 que relaciona la energía en reposo de cualquier partícula de masa m con la velocidad de la luz c.
Tercer postulado: para obtener el operador hamiltoniano se usa la misma regla de cuantización empleada en la ecuación de Schrodinger:
p = -i ħ ∂ /∂r
Al comienzo, no era claro cómo manejar este operador diferencial actuando dentro de una raíz cuadrada, por lo que Dirac se propuso obtener un operador Hamiltoniano lineal en el operador momentum y de allí surgió su cuarto postulado.
Cuarto postulado: para deshacerse de la raíz cuadrada en la fórmula de energía relativista, Dirac propuso la siguiente estructura para E2:
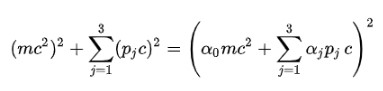
Desde luego, es necesario determinar los coeficientes alfa (α0, α1, α2, α3) para que esto se cumpla.
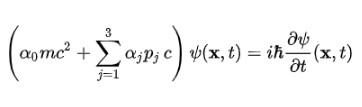
En su forma compacta, la ecuación de Dirac es considerada una de las ecuaciones matemáticas más bellas del mundo:
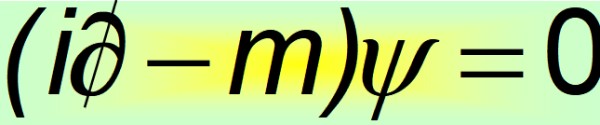
Y es entonces cuando se pone en evidencia que las constantes alfas no pueden ser cantidades escalares. La única forma en que se cumpla la igualdad del cuarto postulado es que sean matrices constantes 4×4, las cuales se conocen como matrices de Dirac:
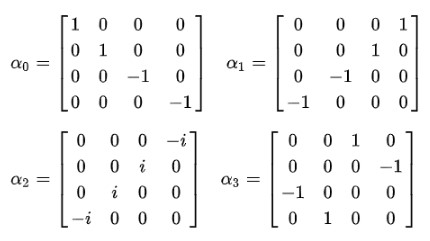
De inmediato se observa que la función de onda deja de ser una función escalar y pasa a ser un vector de cuatro componentes llamado espinor:
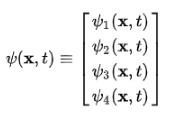
Para obtener el modelo atómico es necesario pasar de la ecuación del electrón libre a la del electrón en el campo electromagnético producido por el núcleo atómico. Esta interacción se toma en cuenta incorporando el potencial escalar Φ y el potencial vectorial A en el hamiltoniano:
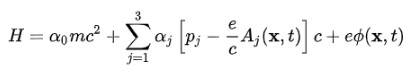
La función de onda (espinor) que resulta de incorporar este hamiltoniano tiene las siguientes características:
– Cumple la relatividad especial, ya que toma en cuenta la energía intrínseca del electrón (primer término del hamiltoniano relativista)
– Tiene cuatro soluciones correspondientes a las cuatro componentes del espinor
– Las dos primeras soluciones se corresponden una al espín +½ y la otra al espín – ½
– Finalmente, las otras dos soluciones predicen la existencia de la antimateria, ya que corresponden a la de los positrones de espines contrarios.
La gran ventaja de la ecuación de Dirac es que las correcciones al Hamiltoniano básico de Schrodinger H(o) pueden desglosarse en varios términos que mostraremos a continuación:
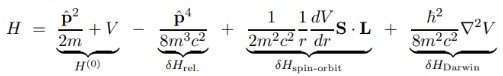
En la expresión anterior V es el potencial escalar, ya que el potencial vector A es nulo si se supone al protón central estacionario y por eso no aparece.
La razón por las que las correcciones de Dirac respecto a las soluciones de Schrodinger en la función de onda son sutiles. Surgen del hecho de que los tres últimos términos del hamiltoniano corregido están todos divididos por la velocidad c de la luz al cuadrado, un número inmenso, lo que hace que estos términos sean numéricamente pequeños.
Usando la ecuación de Dirac-Jordan se encuentran correcciones al espectro de energía del electrón en el átomo de hidrógeno. También se encuentran correcciones para la energía en los átomos con más de un electrón en forma aproximada a través de un metodología conocida como teoría de perturbaciones.
De igual forma, el modelo de Dirac permite encontrar la corrección de estructura fina en los niveles de energía del hidrógeno.
Sin embargo, correcciones más sutiles aún como la estructura hiperfina y el corrimiento de Lamb se obtienen de modelos más avanzados como la teoría cuántica de campos, que nace justamente por las aportaciones del modelo de Dirac.
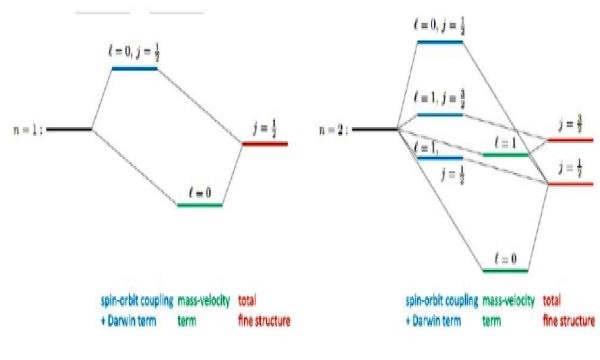
La siguiente figura muestra cómo son las correcciones relativistas de Dirac a los niveles de energía:
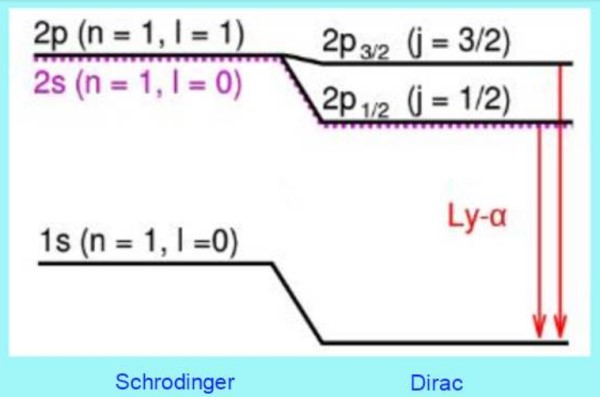
Por ejemplo, las soluciones a la ecuación de Dirac predicen correctamente un corrimiento observado en el nivel 2s. Es la conocida corrección de estructura fina en la línea Lyman – alfa del espectro del hidrógeno (ver figura 3).
Por cierto, la estructura fina es el nombre que recibe en física atómica el desdoblamiento de las líneas del espectro de emisión de los átomos, lo cual es una consecuencia directa del espín electrónico.
Modelo atómico de Schrödinger.
- Atomic theory. Recuperado de wikipedia.org.
- Electron Magnetic Moment. Recuperado de wikipedia.org.
- Quanta: A handbook of concepts. (1974). Oxford University Press. Recuperado de Wikipedia.org.
- Modelo atómico de Dirac Jordan. Recuperado de prezi.com.
- The New Quantum Universe. Cambridge University Press. Recuperado de Wikipedia.org.
