Modelo atómico de Broglie: características y limitaciones
El modelo atómico de Broglie fue propuesto por el físico francés Louis Broglie en 1924. En su tesis doctoral, Broglie aseveró la dualidad onda-partícula de los electrones, sentando las bases de la mecánica ondulatoria. Broglie publicó importantes hallazgos teóricos sobre la naturaleza onda-corpúsculo de la materia a escala atómica.
Posteriormente los enunciados de Broglie fueron demostrados experimentalmente por los científicos Clinton Davisson y Lester Germer, en 1927. La teoría de onda de los electrones de Broglie se fundamenta en la propuesta de Einstein sobre las propiedades ondulatorias de la luz en longitudes de onda cortas.

Broglie anunció la posibilidad de que la materia tuviese un comportamiento similar al de la luz, y sugirió propiedades similares en partículas subatómicas como los electrones.
Cargas eléctricas y órbitas restringen la amplitud, longitud y frecuencia de la onda descrita por los electrones. Broglie explicó el movimiento de los electrones alrededor del núcleo atómico.
Índice del artículo
- 1 Características del modelo atómico de Broglie
- 2 Experimento de Davisson y Germer
- 3 Limitaciones
- 4 Artículos de interés
- 5 Referencias
Para desarrollar su propuesta, Broglie partió del principio de que los electrones tenían una naturaleza dual entre onda y partícula, similar a la luz.
En ese sentido, Broglie realizó un símil entre ambos fenómenos, y con base en las ecuaciones desarrolladas por Einstein para el estudio de la naturaleza ondulatoria de la luz, indicó lo siguiente:
– La energía total del fotón y, en consecuencia, la energía total del electrón, resulta del producto de la frecuencia de la onda y la constante de Plank (6,62606957(29) ×10 -34 Jules x segundos), tal como se detalla en la siguiente expresión:
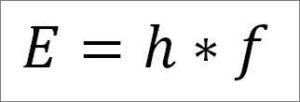
En esta expresión:
E= energía del electrón.
h= constante de Plank.
f= frecuencia de la onda.
– El momento lineal del fotón, y por ende, del electrón, es inversamente proporcional a la longitud de la onda, y ambas magnitudes se relacionan a través de la constante de Plank:
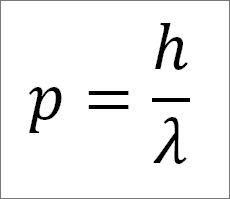
En esta expresión:
p= momento lineal del electrón.
h= constante de Plank.
λ = longitud de la onda.
– El momento lineal es el producto de la masa de la partícula por la velocidad que tiene dicha partícula durante su desplazamiento.
Si la expresión matemática anterior se reestructura en función de la longitud de onda, se tiene lo siguiente:
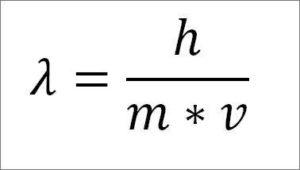
En dicha expresión:
λ = longitud de la onda.
h= constante de Plank.
m= masa del electrón.
v= velocidad del electrón.
Dado que h, la constante de Plank, tiene un valor pequeño, la longitud de onda λ también lo es. En consecuencia, es factible enunciar que las propiedades ondulatorias del electrón se presentan únicamente en niveles atómicos y subatómicos.
– Broglie también se base en los postulados del modelo atómico de Bohr. Según este último, las órbitas de los electrones son limitados y solo pueden ser múltiplos de números enteros. Así:
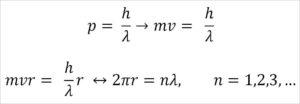
Donde:
λ = longitud de la onda.
h= constante de Plank.
m= masa del electrón.
v= velocidad del electrón.
r= radio de la órbita.
n= número entero.
Según el modelo atómico de Bohr, al cual Broglie adoptó como base, si los electrones se comportan como ondas estacionarias, las únicas órbitas permitidas son aquellas cuyo radio sea igual a un múltiplo entero de la longitud de onda λ.
Por ende, no todas las órbitas cumplen con los parámetros necesarios para que un electrón se movilice a través de estas. He allí el porqué de que los electrones solo puedan desplazarse en órbitas específicas.
La teoría de onda de los electrones de Broglie justificó el éxito del modelo atómico de Bohr para explicar el comportamiento del electrón único del átomo de hidrógeno.
Análogamente, también dio luces sobre por qué este modelo no se ajustó a sistemas más complejos, es decir, átomos con más de un electrón.
La comprobación experimental del modelo atómico de Broglie tuvo lugar 3 años más tarde de su publicación, en 1927.
Los destacados físicos estadounidenses Clinton J. Davisson y Lester Germer confirmaron de forma experimental la teoría de la mecánica ondulatoria.
Davisson y Germer realizaron pruebas de dispersión de un haz de electrones a través de un cristal de níquel y observaron el fenómeno de difracción a través del medio metálico.
El experimento realizado consistió en llevar a cabo el siguiente procedimiento:
– En primera instancia, se colocó un montaje con haz de electrones que tenía una energía inicial conocida.
– Se instaló una fuente de voltaje para acelerar el movimiento de electrones incitando una diferencia de potencial.
– Se dirigió el flujo del haz de electrones hacia un cristal metálico; en este caso, níquel.
– Se midió el número de electrones que impactó en el cristal de níquel.
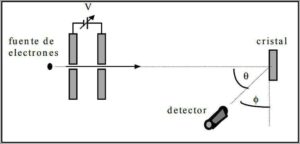
Al finalizar la experimentación, Davisson y Germer detectaron que los electrones se dispersaban en diferentes direcciones.
Al repetir el experimento empleando cristales metálicos con distintas orientaciones, los científicos detectaron lo siguiente:
– La dispersión del haz de electrones a través del cristal metálico era comparable con el fenómeno de interferencia y difracción de los rayos luminosos.
– La reflexión de los electrones sobre el cristal de impacto describía la trayectoria que, teóricamente, debía describir según la teoría de ondas de electrones de Broglie.
En síntesis, el experimento de Davisson y Germer comprobó experimentalmente la naturaleza dual onda-partícula de los electrones.
El modelo atómico de Broglie no predice la ubicación exacta del electrón sobre la órbita en la cual se desplaza.
En este modelo, los electrones se perciben como ondas que se movilizan en toda la órbita sin una ubicación específica, con lo cual se introduce el concepto de orbital electrónico.
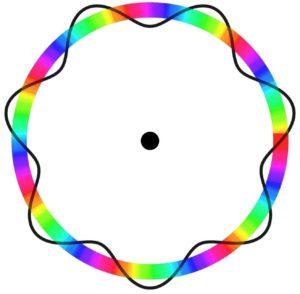
Además, el modelo atómico de Broglie, análogo al modelo de Schrödinger, no considera la rotación de los electrones sobre su mismo eje (spin).
Al obviar el momento angular intrínseco de los electrones, se están dejando de lado las variaciones espaciales de estas partículas subatómicas.
En el mismo orden de ideas, este modelo tampoco toma en cuenta los cambios en el comportamiento de los electrones rápidos como consecuencia de los efectos relativistas.
Modelo atómico de Schrödinger.
Modelo atómico de Dirac Jordan.
- Bohr’s Quantum Theory and De Broglie Waves (s.f.). Recuperado de: ne.phys.kyushu-u.ac.j
- Louis de Broglie – Biographical (1929). © The Nobel Foundation. Recuperado de: nobelprize.org
- Louis-Victor de Broglie (s.f.). Recuperado de: chemed.chem.purdue.edu
- Lovett, B. (1998). Louis de Broglie. Encyclopædia Britannica, Inc. Recuperado de: britannica.com
- Modelo atómico de De Broglie. Universidad Nacional de Educación a Distancia. España. Recuperado de: ocw.innova.uned.es
- Ondas De Materia De Louis De Broglie (s.f.). Recuperado de: hiru.eus
- Von Pamel, O., y Marchisio, S. (s.f.). Mecánica Cuántica. Universidad Nacional de Rosario. Recuperado de: fceia.unr.edu.ar
