Verificar una matriz inversa
Verificar que una matriz tiene matriz inversa es la obtención de la matriz identidad como consecuencia de multiplicar la matriz original por la matriz inversa.
En otras palabras, verificar que una matriz es una matriz inversa es la multiplicación de la matriz original por la matriz inversa y obtener la matriz identidad.
Matriz inversa
Una matriz inversa es la transformación lineal de una matriz mediante la multiplicación del inverso del determinante de la matriz por la matriz adjunta traspuesta.
En otras palabras, una matriz inversa es la multiplicación del inverso del determinante por la matriz adjunta traspuesta.
Propiedad
Una matriz cuadrada X de orden n tendrá una matriz inversa X de orden n, X-1, tal que cumple así:
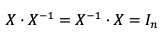
Gracias a esta propiedad podemos verificar que una matriz es una matriz inversa.
El orden de los elementos de la multiplicación no es relevante. Es decir, la multiplicación de una matriz cuadrada cualquiera por su matriz inversa siempre resultará en la matriz identidad del mismo orden.
El orden de la matriz inversa es el mismo que el orden de la matriz original.
Ejercicio
Comprobar que la matriz F tiene matriz inversa y es la matriz U:
En otras palabras, se pide demostrar matemáticamente que
¿Y como se hace eso?
Si multiplicando la matriz U por la matriz F obtenemos la matriz identidad, entonces, querrá decir que la matriz U es la matriz inversa de la matriz F.
La matriz identidad sería tal que:
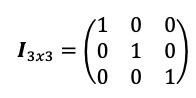
Entonces,
Si se cumple esta igualdad, la matriz F tiene matriz inversa y es la matriz U.
