Matriz traspuesta
Una matriz traspuesta es el resultado de reordenar la matriz original mediante el cambio de filas por columnas y las columnas por filas en una nueva matriz.
En otras palabras, la matriz traspuesta es la acción de seleccionar las filas de la matriz original y reescribirlas como columnas en la nueva matriz e invertir el proceso para las columnas.
Generalmente cuando cambiamos las filas por columnas y las columnas por filas lo indicamos añadiendo un superíndice T o un apóstrofe en el nombre de la matriz original. Si añadimos el superíndice T, deberemos tener presente que estamos trabajando con matrices y que el superíndice no es ningún exponente.
Artículo recomendado: operaciones con matrices.
Fórmula de una matriz traspuesta nxm
Dada una matriz Z cualquiera con n filas y m columnas podemos construir la matriz traspuesta, ZT, que tendrá m filas y n columnas.

Trasposición de una matriz cuadrada

Dependiendo de la tipología de la matriz, el orden de la matriz también cambiará cuando hagamos su traspuesta.
Propiedades
Dada la matriz Z anterior,
- La traspuesta de una matriz traspuesta es la matriz original.
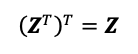
- La suma traspuesta de matrices es igual a la suma de las matrices traspuestas.
- El producto traspuesto de una constante h por una matriz es igual al producto de la constante h por la matriz traspuesta.
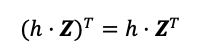
- El producto traspuesto de la multiplicación de matrices es igual al producto de la multiplicación de matrices traspuestas.
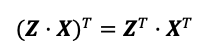
Aplicaciones
Las matrices traspuestas están más presentes de lo que creemos. En econometría encontramos trasposiciones cuando expresamos las matrices en forma cuadrática. Asimismo, la fórmula del estimador de Mínimos Cuadrados Ordinarios (MCO) en forma matricial:
Ejemplo teórico
Encuentra la matriz traspuesta de las siguientes matrices:

