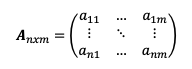Matriz cuadrada
Una matriz cuadrada es una tipología de matriz muy básica que se caracteriza por tener el mismo orden tanto de filas como de columnas.
En otras palabras, una matriz cuadrada tiene el mismo número de filas (n) y el mismo número de columnas (m).
Representación de una matriz cuadrada
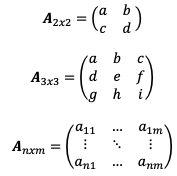
Podemos crear infinitas combinaciones de matrices cuadradas siempre y cuando respetemos la restricción de que el número de columnas y filas tiene que ser el mismo.
Matriz cuadrada de orden n
Dado que en una matriz cuadrada el número de filas (n) es igual al número de columnas (m), matemáticamente decimos que n=m.
Entonces, partiendo de esta igualdad, basta con solo indicar el número de filas (n) que tiene la matriz.
¿Por qué? Pues porque sabiendo el número de filas (n) también sabremos el número de columnas (m) dado que n=m.
El orden nos indica el número de filas (n) y columnas (m) que tiene una matriz. En el caso de la matriz cuadrada, con tan solo indicando el orden de las filas (n) ya sabremos el orden de las columnas (m). Entonces, cuando nos digan que una matriz cuadrada es de orden n, querrá decir que esta matriz tiene n filas y n columnas dado que n=m y m=n.
Diferenciar una matriz cuadrada de otras matrices no cuadradas
¿Cómo nos podemos acordar que una matriz cuadrada tiene el mismo número de filas y columnas?
Pensemos en un cuadrado. Es decir, los cuadrados son famosos por tener los lados de la misma longitud. Entonces, una matriz cuadrada también tendrá esta característica: el número de filas y columnas coincidirán.
A parte de la visión analítica, desde la visión geométrica, una matriz cuadrada también se parecerá a un cuadrado:
Matriz A: forma cuadrado => Matriz cuadrada.
Matriz B: forma rectángulo => Matriz no cuadrada.
Matriz C: forma rectángulo => Matriz no cuadrada.
Aplicaciones
La matriz cuadrada es la base de muchos otros tipos de matrices como la matriz identidad, la matriz triangular, la matriz inversa y la matriz simétrica. Además, también es la base para operaciones complejas como la descomposición de Cholesky o la descomposición LU, ambas muy utilizadas en finanzas.
La utilización de matrices en econometría facilita muchos los cálculos cuando las regresiones lineales son regresiones lineales múltiples. En estos casos, todas las variables y coeficientes pueden expresarse en forma matricial y ayudan en la comprensión del estudio.
Ejemplo teórico
Matriz cuadrada de orden 2: 2 filas y 2 columnas.
Matriz cuadrada de orden 3: 3 filas y 3 columnas.
Matriz cuadrada de orden n: n filas y n columnas (n=m):