Matriz inversa de orden 2
Una matriz inversa es la transformación lineal de una matriz mediante la multiplicación del inverso del determinante de la matriz por la matriz adjunta traspuesta.
En otras palabras, una matriz inversa es la multiplicación del inverso del determinante por la matriz adjunta traspuesta.
Artículos recomendados: determinante de una matriz, matriz cuadrada, diagonal principal y operaciones con matrices.
Dada una matriz X cualquiera tal que
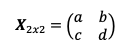
Fórmula matriz inversa de una matriz de orden 2
Entonces, la matriz inversa de X será
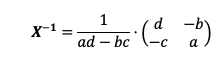
Mediante esta fórmula obtenemos la matriz inversa de una matriz cuadrada de orden 2.
La fórmula anterior también puede expresarse mediante el determinante de la matriz.
Fórmula matriz inversa de una matriz de orden 2
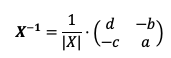
Las dos líneas paralelas alrededor de X en el denominador indican que es el determinante de la matriz X.
Cuando una matriz cuadrada tiene matriz inversa decimos que es una matriz regular.
Requisitos
Para encontrar la matriz inversa de una matriz de orden n necesitamos cumplir con los siguientes requisitos:
- La matriz tiene que ser una matriz cuadrada.
El número de filas (n) tiene que ser el mismo que el número de columnas (m). Es decir, el orden de la matriz tiene que ser n dado que n=m.
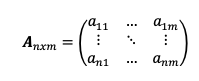
- El determinante debe ser distinto de cero (0).
El determinante de la matriz debe ser distinto de cero (0) dado que participa en la fórmula como denominador. Si el denominador fuera un cero (0) tendríamos una indeterminación.
Si el denominador (ad – bc) = 0, es decir, el determinante de la matriz X es igual a cero (0), entonces la matriz X no tiene matriz inversa.
Propiedad
Una matriz cuadrada X de orden n tendrá una matriz inversa X de orden n, X-1, tal que cumple que
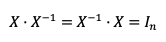
El orden de los elementos de la multiplicación no es relevante, es decir, la multiplicación de una matriz cuadrada cualquiera por su matriz inversa siempre resultará en la matriz identidad del mismo orden.
En este caso, el orden de la matriz X es 2. Entonces, podemos reescribir la propiedad anterior como:
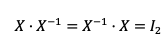
Ejemplo práctico
Encuentra la matriz inversa de la matriz V.
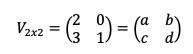
Para resolver este ejemplo podemos aplicar la fórmula o primero calcular el determinante y luego sustituirlo.
Fórmula
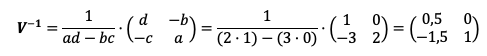
Fórmula con determinante
Primero calculamos el determinante de la matriz V y luego lo sustituimos en la fórmula.
Entonces, obtenemos que el determinante de la matriz V es distinto de cero (0) y podemos decir que la matriz V sí tiene matriz inversa.
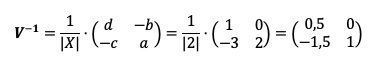
Obtenemos el mismo resultado utilizando la fórmula o primero calculando el determinante y luego sustituirlo.
El orden de la matriz inversa es el mismo que el orden de la matriz original. En este caso, tendremos el mismo número de filas n y de columnas m tanto en la matriz V y V-1.

 José Antonio Ludeña
José Antonio Ludeña