Matriz adjunta
Una matriz adjunta es una transformación lineal de la matriz original a través del determinante de los menores y su signo y se utiliza principalmente para obtener la matriz inversa.
En otras palabras, una matriz adjunta es el resultado de cambiar el signo del determinante de cada uno de los menores de la matriz original en función de la posición del menor dentro de la matriz.
La matriz adjunta de una matriz W se representa como Adj(W).
El orden de la matriz original y la matriz adjunta coinciden, es decir, la matriz adjunta tendrá el mismo número de columnas y filas que la matriz original.
Artículos recomendados: diagonal principal, operaciones con matrices, matriz cuadrada.
Dada una matriz W cualquiera de orden n definimos los elementos de la fila i y los elementos de la columna j de W como wij.
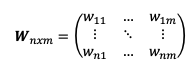
Fórmula matriz adjunta
La matriz adjunta de la matriz W se obtiene a partir de:
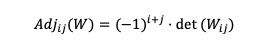
En las matrices de orden 2, Wij es el elemento w que corresponde a la fila i y a la columna j. Entonces, det (Wij) es el elemento w de la fila i y la columna j.
En las matrices de orden mayor o igual a 3, Wij es el menor que se obtiene de eliminar la fila i y la columna j de la matriz W. Entonces, det (Wij) es el determinante del menor Wij.
Es importante tener en cuenta el cambio de signo que debemos aplicar cuando la suma de las filas y de las columnas con las que estamos trabajando suman un número impar. En el caso de que sumen un número par, el signo negativo producirá un efecto neutro sobre el menor.
Aplicaciones
La matriz adjunta se aplica para obtener la matriz inversa de una matriz con determinante distinto de cero (0). Entonces, para obtener la matriz inversa deberemos exigir que la matriz sea cuadrada e invertible, es decir, que sea una matriz regular. En cambio, para calcular la matriz adjunta solo tenemos que encontrar los menores de la matriz.
Ejemplo teórico
Matriz de orden 2
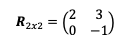
- Sustituimos los elementos de la matriz en la fórmula anterior.

Matriz de orden 3
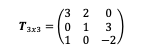
- Sustituimos los elementos de la matriz en la fórmula anterior.
- Calculamos el determinante de cada menor.

