Determinante de una matriz
El determinante de una matriz de dimensión mxn es el resultado de restar la multiplicación de los elementos de la diagonal principal con la multiplicación de los elementos de la diagonal secundaria.
En otras palabras, el determinante de una matriz 2×2 se obtiene dibujando una X sobre sus elementos. Primero dibujamos la diagonal que empieza por arriba en lado izquierdo de la X (diagonal principal). Después dibujamos la diagonal que empieza por arriba en el lado derecho de la X (diagonal secundaria).
Para calcular el determinante de una matriz, necesitamos que su dimensión tenga el mismo número de filas (m) y de columnas (n). Por tanto, m=n. La dimensión de una matriz se representa como la multiplicación de la dimensión de la fila con la dimensión de la columna.
Existen otras maneras más complejas para calcular el determinante de una matriz de dimensión mayor de 2×2. Estas formas se conocen como la regla de Laplace y la regla de Sarrus.
El determinante se puede indicar de dos formas:
- Det(Z)
- |Zmxn|
Denominamos (m) para la dimensión de las filas y (n) para la dimensión de las columnas. Entonces, una matriz mxn tendrá mfilas y ncolumnas:
- irepresenta cada una de las filas de una matriz Zmxn.
- jrepresenta cada una de las columnas de una matriz Zmxn.
Artículos recomendados: tipologías de matrices, matriz invertida.
Propiedades de los determinantes
- |Zmxn| es igual al determinante de una matriz Zmxn traspuesta:

- El determinante inverso de una matriz Zmxninvertible es igual al determinante de una matriz Zmxn inversa:
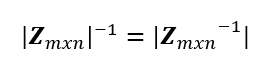
- El determinante de una matriz singularSmxn(no invertible) es 0.
Smxn=0
- |Zmxn|, donde m=n, multiplicado por una constante h cualquiera es:
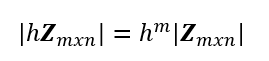
- El determinante del producto de dos matrices Zmxny Xmxn, donde m=n, es igual al producto de determinantes de Zmxny Xmxn
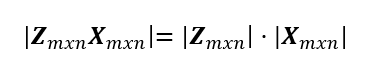
Ejemplo práctico
Matriz de dimensión 2×2
Una matriz de dimensión 2×2 tiene como determinante la resta del producto de los elementos de la diagonal principal con el producto de los elementos de la diagonal secundaria.
Definimos Z2×2 como:
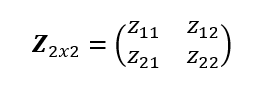
El cálculo de su determinante sería:
Ejemplo del cálculo de determinante
El determinante de la matriz X2×2es 14.
El determinante de la matriz G2×2es 0.
