Dispersión estadística

Por tanto, las medidas de dispersión van a acompañar siempre a esa media o promedio.

De esta forma, estarían informando de la variabilidad o dispersión de los datos en relación a ella. A mayores valores, como veremos a continuación, mayor dispersión estadística.

Cuando queremos llevar a cabo un análisis descriptivo, en primer lugar calculamos las medidas resumen de posición. Las más habituales son la media, mediana, moda o cuartiles, deciles, quintiles o percentiles. Además, necesitamos saber la dispersión estadística.

Las medidas de dispersión aportan información muy relevante. Si la dispersión es muy elevada afecta a la media y esta deja de ser representativa del grupo como medida resumen. Por eso, normalmente ambos datos van juntos.

Existen diversas medidas de dispersión que permiten su medición. Veamos un resumen de las más relevantes. Las hemos analizado con mas detalle aquí.

• Rango: No es más que la diferencia entre el menor y el mayor valor de la distribución.
• Desviación media: Sería el equivalente al promedio de las diferentes desviaciones de cada dato respecto a la media.
• Varianza y desviación típica: Son las medidas de dispersión más conocidas. Suele utilizarse la segunda que es más fácil de calcular (raíz de la varianza) y de interpretar. Se expresan en valores absolutos.
• Coeficiente de variación: En este caso, se calcula con la desviación típica y la media, y sirve para comparar, ya que se expresa en valores relativos (%).

Para terminar, vamos a ver un ejemplo de diez países ficticios y su PIB.

Podemos observar que son muy diferentes en lo que se refiere a su PIB. Desde el mayor, con 7.000 millones de unidades, hasta el menor, con 2.500 millones.

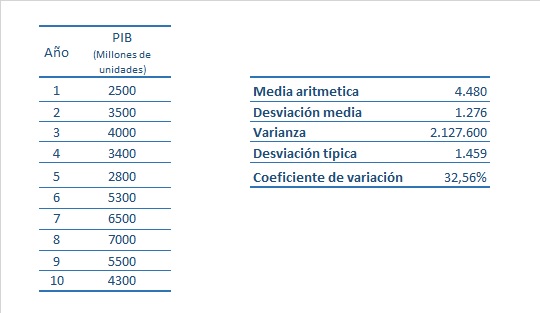
Vemos que la media son casi 4.500 millones, pero las medidas de dispersión son muy elevadas. Por un lado, la desviación media, de casi 1.500 millones de unidades. La varianza, que no aporta gran cosa, pero permite el cálculo de la desviación típica de casi 1.500 millones de unidades. Por último, un coeficiente de variación de casi el 33%.

Podemos decir que la dispersión estadística es muy elevada y la media no es representativa. Algo que se puede comprobar porque son pocos datos y se observan países con un alto PIB y otros con uno bajo. Pero imaginemos los 194 reconocidos por la ONU, ahí sí son bastante útiles, ¿verdad?