Decil

El decil, por tanto, no es más que un tipo de cuantil, o una serie de particiones que se llevan a cabo en los datos de una muestra o población.

Además, estos deben ir ordenados de menor a mayor. De esta forma, el decil también irá en ese mismo orden.

El decil, como cualquier otro cuantil, puede calcularse para datos agrupados o no agrupados. Para los primeros, existen ciertas fórmulas que podemos encontrar en manuales de estadística básica. Para los segundos, el proceso es relativamente más sencillo, sobre todo si disponemos de una hoja de cálculo. En el ejemplo veremos esto con algo más de detalle.

Debemos decir que, en el caso de datos no agrupados, se utiliza una expresión matemática para situar el valor de dicho decil. Esta es relativamente sencilla, ya que se basa en que las nueve partes de la distribución tienen el mismo tamaño.

Por tanto, lo que se hace es utilizar el valor concreto si obtenemos un número entero, o un promedio, si el número tiene decimales.

Veamos una representación gráfica de esta medida de posición no central con la fórmula que podemos utilizar en una hoja de cálculo:

Los deciles tienen una serie de características, como las que mostramos a continuación:

• Como estadísticos de posición, son útiles para conocer qué lugar ocupan los datos en una distribución. Así, el decil 8 es el límite superior de los datos que representan el 80% del total.
• Por otro lado, permiten conocer cuáles de ellos se sitúan en los niveles más altos (>90%) y en los más bajos (<10%).
• Son muy frecuentes en comparaciones económicas, como niveles de renta, salarios o ingresos.
• Además, junto a los cuartiles, quintiles o percentiles, son los cuantiles más utilizados en estadística descriptiva.

Imaginemos que queremos estudiar los ingresos per cápita anuales en un país (con datos ficticios). Para ello, hemos escogido una muestra que, a su vez, hemos agrupado en ciertos valores medios.

A continuación, calculamos este estadístico y observamos qué sucede, pudiendo obtener información relevante. En el ejemplo, vamos a utilizar como moneda de referencia el euro.

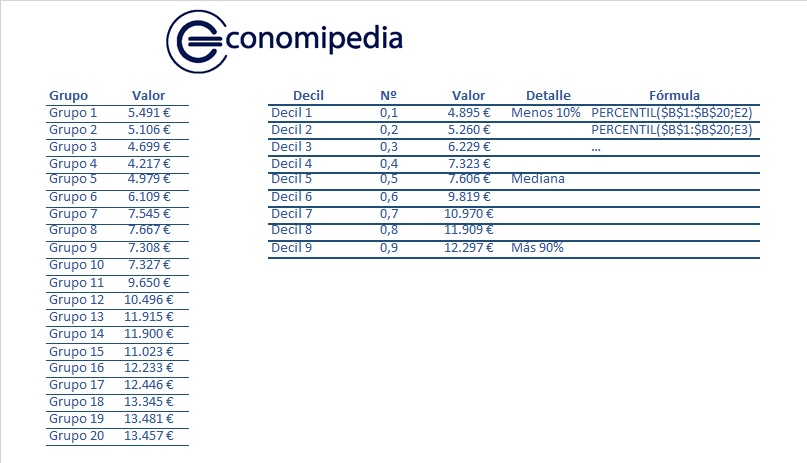
Atendiendo al ejemplo, en primer lugar, vemos que el 10% de la población con menos ingresos se sitúa en algo menos de los 5.000 €. Por otro lado, en el lado opuesto, el 90% que más ingresa, obtiene 12.297 €. Con estos datos, podemos comprobar la diferencia entre ambos.

De esta forma, también, la mediana sería 7.606 € y se corresponde con el decil cinco (D5). Esta nos indicaría el salario mediano del país.

En definitiva y como vemos, hablamos de un concepto muy útil para el análisis.