Desviación estándar o típica
La desviación estándar o desviación típica es una medida que ofrece información sobre la dispersión media de una variable. La desviación estándar es siempre mayor o igual que cero.
Para entender este concepto necesitamos analizar 2 conceptos fundamentales.
- Esperanza matemática, valor esperado o media: Es la media de nuestra serie de datos.
- Desviación: La desviación es la separación que existe entre un valor cualquiera de la serie y la media.
Ahora, entendiendo estos dos conceptos la desviación típica se calculará de forma similar a la media. Pero tomando como valores las desviaciones. Y aunque este razonamiento es intuitivo y lógico tiene un fallo que vamos a comprobar con el siguiente gráfico.
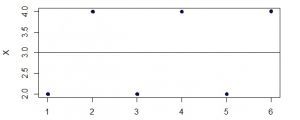
En la imagen anterior tenemos 6 observaciones, es decir, N = 6. La media de las observaciones está representa por la línea negra situada en el centro del gráfico y es 3. Entenderemos por desviación, la diferencia que existe entre cualquiera de las observaciones y la línea negra. Así pues, tenemos 6 desviaciones.
- Desviación -> (2-3) = -1
- Desviación -> (4-3) = 1
- Desviación -> (2-3) = -1
- Desviación -> (4-3) = 1
- Desviación -> (2-3) = -1
- Desviación -> (4-3) = 1
Como podemos ver si sumamos las 6 desviaciones y dividimos entre N (6 observaciones), el resultado es cero. La lógica sería que la desviación media fuese de 1. Pero una característica matemática de la media respecto a los valores que la forman es, precisamente, que la suma de las desviaciones es cero. ¿Cómo arreglamos esto? Elevando al cuadrado las desviaciones
Fórmulas para calcular la desviación típica
La primera es elevando al cuadrado las desviaciones, dividir entre el número total de observaciones y por último hacer la raíz cuadrada para deshacer el elevado al cuadrado, tal que:
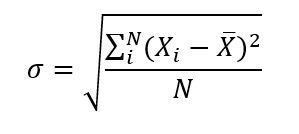
Alternativamente existiría otra forma de calcularla. Sería haciendo un promedio de la suma de los valores absolutos de las desviaciones. Es decir, aplicar la siguiente fórmula:
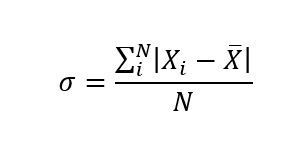
Sin embargo, esta fórmula no es una alternativa de la desviación típica pues arroja diferentes resultados. En realidad, la fórmula anterior es la desviación respecto de la media. La desviación estándar o típica y la desviación respecto de la media tienen similitudes pero no son lo mismo. A esta última forma se le conoce como desviación media.
Ejemplo de cálculo de la desviación estándar
Vamos a comprobar como, con cualquiera de las dos fórmulas expuestas, el resultado de la desviación típica o desviación media es el mismo.
Según la fórmula de la varianza (raíz cuadrada):
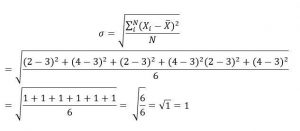
Según la fórmula del valor absoluto:
Tal como dictaba el cálculo intuitivo. La desviación media es de 1. Pero, ¿no habíamos dicho que la fórmula del valor absoluto y de la desviación típica daban valores diferentes? Así es, pero hay una excepción. El único caso en que la desviación estándar y la desviación respecto de la media ofrecen el mismo resultado es el caso en que todas las desviaciones son igual a 1.
La relación de la desviación típica con la varianza
En definitiva la varianza no es más que la desviación estándar al cuadrado. O lo que viene a ser lo mismo, la desviación típica es la raíz cuadrada de la varianza. Se relacionan de la siguiente forma:
Tras esta imagen, queda claro que toda la fórmula que está dentro de la raíz cuadrada es la varianza. La razón por la que es necesario entender que esa parte se conoce como varianza es que se utiliza en otras fórmulas para calcular otras medidas. Así pues aunque la desviación típica sea más intuitiva para interpretar resultados, es imperativo cómo se calcula la varianza.
