Percentil
El percentil es una medida estadística de posición, que divide la distribución ordenada de los datos en cien partes iguales.
Esta medida de posición no central aporta información sobre el porcentaje de observaciones de una variable, ordenados de menor a mayor, que se sitúan por debajo del valor de este.
De esta forma, el percentil 20 (P20) sería el valor de la variable, situado este en el límite de los 20 primeros.
¿Cómo se calcula el percentil?
Como todos los cuantiles, el percentil se puede calcular para datos agrupados o no. Para los primeros, existen fórmulas algo complejas que podemos encontrar en manuales de estadística. Para los segundos, lo más fácil es utilizar una hoja de cálculo.
En la imagen podemos observar una forma de representación. El rectángulo principal representa los datos ordenados de menor a mayor, y los de color azul claro los diferentes percentiles.
Hemos mostrado los tres más relevantes. Sobre todo el P50, que se corresponde con la mediana.
También incluimos la fórmula para su cálculo.
Característica del percentil
Veamos algunas de las características más relevantes del percentil.
- En primer lugar, es similar a otras medidas de posición no central. Por tanto, nos informa sobre la posición de un dato respecto a otros.
- Por otro lado, en muchas situaciones aporta información más detallada que otros. Por ejemplo, algunos índices de impacto de revistas científicas utilizan este en lugar del cuartil.
- Además, es de mucha utilidad para agrupar una gran cantidad de datos. Cuando trabajamos con muchos casos, los otros cuantiles pueden arrojar grupos demasiado numerosos y difíciles de interpretar.
- Sin embargo, tiene un inconveniente relacionado con lo anterior. No es útil para muestras con pocos casos, ya que los grupos serían demasiado pequeños. Por eso, en estas circunstancias se recomiendan otros como el cuartil o el decil.
Ejemplo de percentil y el índice de impacto
Las revistas científicas miden su importancia con los llamados índices de impacto. Este es un indicador muy utilizado en la ciencia.
El más conocido es el JCR que divide las publicaciones en cuartiles. Sin embargo, el segundo en importancia es el SJR que lo hace en percentiles.
Así pues, imaginemos un ejemplo ficticio como el que aparece en la imagen.
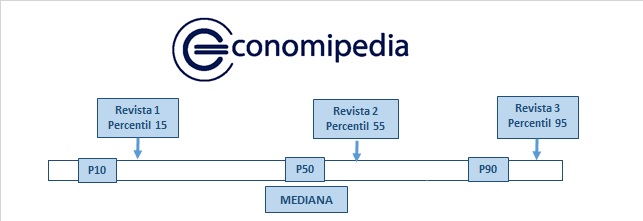
Podemos observar que la que hemos llamado revista 1 se sitúa en el P15, mientras la 2 lo hace en el P55 y la 3 en el P95.
En este caso, la de mayor impacto es la tres, ya que los índices estarían ordenados de menor a mayor.
