Quintil

El quintil es una medida de posición no central, y se utiliza en estadística descriptiva. Por otro lado, hay que tener en cuenta que tendremos cuatro quintiles.

Asimismo, es muy útil en diversos análisis como el económico. Sobre todo en aquellos que guardan relación con los ingresos de la población.

El quintil se calcula para datos agrupados o no agrupados.

En el artículo nos centraremos en los no agrupados, ya que el proceso puede llevarse a cabo con una hoja de cálculo.

Este es relativamente sencillo, pues hay que dividir la distribución en cinco partes y se puede hacer como aparece en la imagen que mostramos a continuación:

En el ejemplo, la mediana no coincide con ningún valor. De hecho, se sitúa entre el segundo y el tercero.

Como vemos, se utiliza la misma fórmula del percentil. El rango son los datos a analizar y como parámetros tendremos 0.2 (1/5), 0.4 (2/5), 0.6 (3/5) y 0.8 (4/5) para cada quintil.

Por tanto, podemos comprobar que los quintiles son similares a los deciles o los percentiles.

A continuación, veamos algunas de las características más relevantes de un quintil.

• A diferencia de otros como el cuartil o el percentil, que representan el 25% o el 1% de una distribución de datos, el quintil representa datos agrupados al 20%. Esto es muy útil en ciertos casos donde conviene hacer cinco grupos.
• Es muy utilizado en economía, para clasificar una población en función de sus ingresos. Se ordenan de menor a mayor renta. De esta forma, el primer quintil será el grupo de los de ingresos más bajos, mientras que el cuarto hará referencia a aquellos que tienen los ingresos más elevados.
• El inconveniente es que no suele ser de utilidad en casos donde queremos hacer grupos mayores, o nos interesa que uno de los valores coincida con la mitad de la distribución (la mediana). Para estas situaciones es mejor usar otros cuantiles como el cuartil.

Imaginemos que queremos estudiar una distribución de salarios en una población.

Estamos utilizando valores ficticios a modo de ejemplo y en miles de unidades anuales.

Por ello, miremos la figura y después la comentamos:

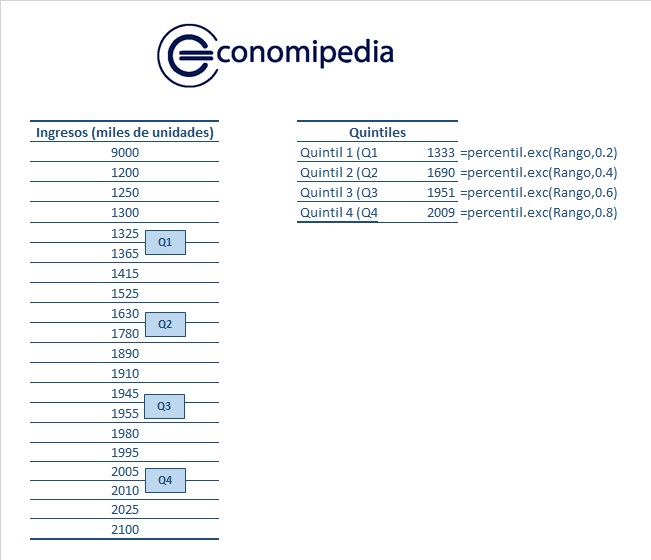
En la imagen, observamos que los casos con menores ingresos se sitúan por debajo del quintil 1, y su valor límite sería de 1333.

Por otro lado, los datos con mayores ingresos son los que aparecen a partir del quintil 4, con un valor límite de 2009.

Esta medida estadística, por tanto, nos da información relevante sobre una serie de datos ordenados.