Varianza
La varianza es una medida de dispersión que representa la variabilidad de una serie de datos respecto a su media. Formalmente se calcula como la suma de los residuos al cuadrado divididos entre el total de observaciones.
También se puede calcular como la desviación típica al cuadrado. Dicho sea de paso, entendemos como residuo a la diferencia entre el valor de una variable en un momento y el valor medio de toda la variable.
Antes de ver la fórmula de la varianza, debemos decir que la varianza en estadística es muy importante. Ya que aunque se trata de una medida sencilla, puede aportar mucha información sobre una variable en concreto.
Fórmula para calcular la varianza
La unidad de medida de la varianza será siempre la unidad de medida correspondiente a los datos pero elevada al cuadrado. La varianza siempre es mayor o igual que cero. Al elevarse los residuos al cuadrado es matemáticamente imposible que la varianza salga negativa. Y de esa forma no puede ser menor que cero.
Donde
- X: variable sobre la que se pretenden calcular la varianza
- xi: observación número i de la variable X. i puede tomará valores entre 1 y n.
- n: número de observaciones.
- x̄: Es la media de la variable X.
O lo que es lo mismo:
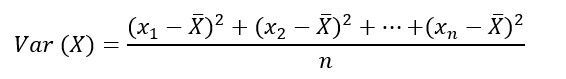
¿Por qué se elevan al cuadrado los residuos?
La razón por la que los residuos se elevan al cuadrado es sencilla. Si no se elevasen al cuadrado, la suma de residuos sería cero. Es una propiedad de los residuos. Así pues para evitarlo, tal como ocurre con la desviación típica se elevan al cuadrado. El resultado es la unidad de medida en la que se miden los datos pero elevada al cuadrado.
Por ejemplo, si tuviésemos datos sobre los salarios de un conjunto de personas en euros, el dato que arroja la varianza sería en euros cuadrados. Para que tenga sentido la interpretación calcularíamos la desviación típica y pasaríamos el dato a euros.
- Desviación -> (2-3) = -1
- Desviación -> (4-3) = 1
- Desviación -> (2-3) = -1
- Desviación -> (4-3) = 1
- Desviación -> (2-3) = -1
- Desviación -> (4-3) = 1
Si sumamos todas las desviaciones el resultado es cero.
¿Qué diferencia existe entre la varianza y la desviación típica?
Una cuestión que se podría plantear, y con razón, sería la diferencia entre varianza y desviación típica. En realidad, vienen a medir lo mismo. La varianza es la desviación típica elevada al cuadrado. O al revés, la desviación típica es la raíz cuadrada de la varianza.
La desviación típica se hace para poder trabajar en las unidades de medida iniciales. Claro que, como es normal, uno puede preguntarse, ¿de qué sirve tener como concepto la varianza? Bien, aunque la interpretación del valor que arroja no nos da demasiada información, su cálculo es necesario para obtener el valor de otros parámetros.
Para calcular la covarianza necesitamos la varianza y no la desviación típica, para calcular algunas matrices econométricas se utiliza la varianza y no la desviación típica. Es una cuestión de comodidad a la hora de trabajar con los datos en según qué cálculos.
Ejemplo de cálculo de la varianza
Vamos a acuñar una serie de datos sobre salarios. Tenemos cinco personas, cada uno con un salario diferente:
Juan: 1.500 euros
Pepe: 1.200 euros
José: 1.700 euros
Miguel: 1.300 euros
Mateo: 1.800 euros
La media del salario, la cual necesitamos para nuestro cálculo, es de ((1.500 + 1.200 + 1.700 + 1.300 + 1.800) /5) 1.500 euros.
Dado que la fórmula de la varianza en su forma desglosada se formula como sigue:
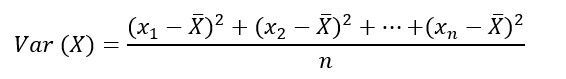
Obtendremos que se debe calcular tal que:
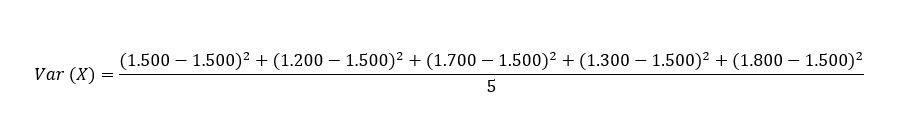
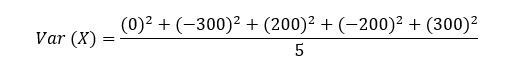
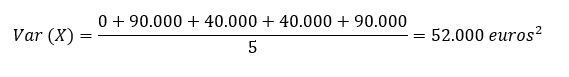
El resultado es de 52.000 euros al cuadrado. Es importante recordar que siempre que calculamos la varianza tenemos las unidades de medida al cuadrado. Para pasarlo a euros, en este caso tendríamos que realizar la desviación típica. El resultado aproximado sería de 228 euros. Esto quiere decir que, en media, la diferencia entre los salarios de las distintas personas será de 228 euros.

 José Antonio Ludeña
José Antonio Ludeña