Definición de coseno
La idea de coseno se emplea en el terreno de la geometría. Coseno, en este marco, es el seno del complemento de un arco o de un ángulo, indica la Real Academia Española (RAE) en su diccionario. La abreviatura oficial de esta función trigonométrica es cos, y de esta forma la encontramos en las ecuaciones y en las calculadoras.
Cabe destacar que el seno es el resultado de dividir el cateto que resulta opuesto a un ángulo y la hipotenusa (en un triángulo rectángulo, el lado mayor es la hipotenusa, mientras que los otros dos –que forman el ángulo de 90º– se denominan catetos). El complemento, por su parte, es el ángulo que, sumándose a otro, completa un ángulo de 90°.
Estos conceptos pertenecen a la rama de las matemáticas conocida como trigonometria, la cual se enfoca en el análisis de las denominadas razones trigonométricas, entre las cuales se encuentran las siguientes cuatro, además del seno y el coseno: tangente, secante, cotangente y cosecante.
En el colegio secundario, la trigonometría suele incluirse en la última etapa del programa, ya que se trata de una parte muy compleja y difícil de entender para quienes no poseen un gusto legítimo por los números. Su intervención en el resto de las ramas de las matemáticas a veces es directa, y otras veces, indirecta; a grandes rasgos, podemos decir que su aplicación tiene lugar siempre que se vuelve necesario realizar mediciones con un alto grado de prescisión.
Supongamos que tenemos un triángulo rectángulo ABC, con un ángulo de 90º y dos ángulos de 45º. Dividiendo uno de los catetos opuestos a un ángulo de 45º y la hipotenusa, obtendremos el seno y luego podemos calcular el coseno.
Otro modo más sencillo de calcular el coseno en un triángulo rectángulo es dividiendo el cateto adyacente a un ángulo agudo y la hipotenusa. El seno, por su parte, se obtiene al dividir el cateto opuesto a la hipotenusa, mientras que la tangente implica la división del cateto opuesto y el cateto adyacente. Estas tres funciones (coseno, seno y tangente) son las más relevantes de la trigonometría.
Si un triángulo tiene una hipotenusa de 4 centímetros, un cateto opuesto de 2 centímetros y un cateto adyacente de 3,4 centímetros, su coseno será 0,85:
Coseno = Cateto adyacente / hipotenusa
Coseno = 3,4 / 4
Coseno = 0,85
La función secante, por otra parte, implica la división de 1 por el coseno. En el ejemplo anterior, la secante es 1,17.
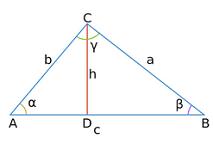La ley de cosenos, que también se conoce como el teorema del coseno, es una generalización del conocido teorema de Pitágoras. Se trata de la relación que se puede establecer entre uno de los lados de un triángulo rectángulo con los dos restantes y con el coseno del ángulo que éstos forman.
En un triángulo ABC, con los ángulos α, β, γ y los lados a, b, c (opuestos a los anteriores, en orden respectivo), el teorema del coseno se puede definir como se aprecia en la imagen: c elevado al cuadrado es igual a la suma de a al cuadrado y b al cuadrado, menos el doble del producto ab cosγ.
Otra forma de definir el coseno consiste en entenderlo como:
* una función par: en matemáticas, esta clasificación la reciben las funciones de variable real tomando en cuenta su paridad. Existen tres posibilidades: pueden ser pares, impares o bien no tener paridad;
* una función continua: se trata de una función matemática en la cual los puntos cercanos al dominio acarrean una serie de variaciones pequeñas en sus valores;
* una función trascendente: es una función que no puede satisfacer una ecuación polinómica con coeficientes que sean polinomios (un polinomio es una expresión compuesta por una suma de productos de constantes y variables entre sí).