Definición de seno
Seno, un concepto con origen etimológico en la palabra latina sinus, tiene diversos usos. La primera acepción que reconoce el diccionario de la Real Academia Española (RAE) refiere al agujero, el hueco o la abertura de algo. Por extensión, se asocia la idea de seno al interior de una cosa.
Por ejemplo: “Los pobladores nativos creían que, en el seno del volcán, habitaban terribles monstruos”, “El petróleo brotó del seno de la tierra y ya nada fue igual en la región”, “No podemos permitir actitudes tan dañinas en el seno de nuestra comunidad”.

Se llama seno al pecho de la mujer.
Seno como pecho femenino
El término seno también hace referencia al pecho de una mujer. De este modo, pueden asociarse los senos a las mamas o las glándulas mamarias: “La modelo causó revuelo al desfilar con los senos al descubierto”, “Es importante que, a la hora de la ducha, las mujeres se palpen los senos para una eventual detección temprana del cáncer de mama”, “La pelota me golpeó en el seno izquierdo”.
A partir de este significado, seno se emplea para nombrar al regazo de la madre o a todo aquello que brinda resguardo, ayuda o protección: “Doña Elvira mantuvo a su nieto en su seno durante horas, hasta que el pequeño se tranquilizó”, “Estoy agradecido a este país que me acogió en su seno cuando llegué escapando de la guerra”, “Ante un problema, un niño siempre acude al seno de su progenitora”.
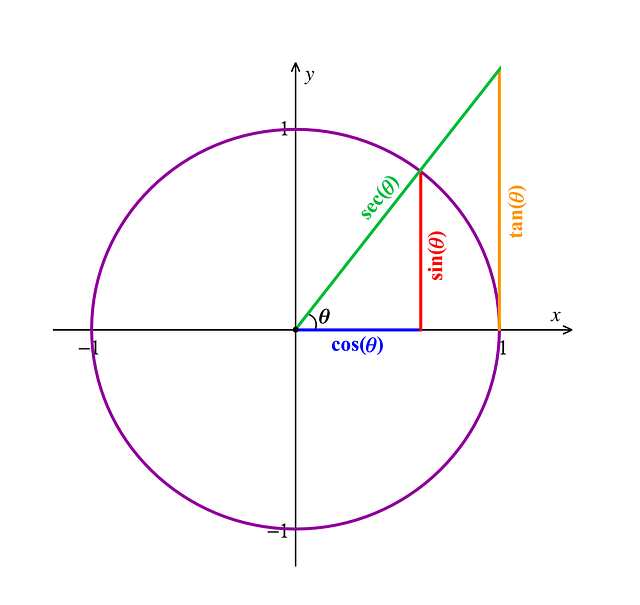
Entre las funciones trigonométricas de los ángulos rectángulos, aparece el seno.
Una función trigonométrica
En el contexto de las matemáticas, el seno es una función trigonométrica de un triángulo rectángulo, que se calcula a partir de la división del cateto opuesto por la hipotenusa. De este modo, el seno de un triángulo cuyo cateto opuesto mide 20 centímetros y su hipotenusa, 60 centímetros, es igual a 0,33.
La trigonometría define la ley de los senos como una relación de proporcionalidad (o sea, una razón o relación constante entre magnitudes que pueden ser medidas) entre la longitud de cada lado de un triángulo y el seno de cada ángulo opuesto respectivo. Esto también se conoce con el nombre de teorema de los senos y suele presentarse con la siguiente definición: si en el triángulo ABC (los nombres de sus ángulos) entendemos que a, b y c son las longitudes de sus lados opuestos, podemos decir que a / sin A = b / sin B = c / sin C.
Los ángulos A, B y C también pueden aparecer como α, β y γ (alfa, beta y gama), las tres primeras letras del alfabeto griego. Cabe mencionar que no muchos conocen su demostración, a pesar de que ésta sea muy sencilla y de tratarse de una de las leyes trigonométricas más usadas. Veamos, por lo tanto, su demostración.
Demostración de la ley
En primer lugar debemos dibujar el triángulo ABC y denotar su circuncentro O, o sea el centro de su circunferencia circunscrita, la cual en este caso se define como aquella que pasa por todos los vértices del triángulo, y dibujar también dicha circunferencia.
El paso siguiente consiste en trazar una línea que contenga el segmento BO y que continúe hasta atravesar el lado AC y corte la circunferencia, para dar lugar al diámetro BP. En este momento deberíamos observar un triángulo recto, PCB. Los ángulos P y A son congruentes, ya que los dos son inscritos y abren BC. Un ángulo inscrito es convexo y su vértice se encuentra en una circunferencia, además de estar constituido por semirrectas cuerdas o secantes de ésta. Todo esto da lugar a la siguiente igualdad, según la función seno: sin A = sin P = BC / BP = a / 2R, siendo R el radio.
Finalmente, al despejar 2R podemos obtener a / sin A = 2R y si repetimos esto con otros dos diámetros, uno a partir de A y otro, de C, podemos confirmar que todas las fracciones resultantes son iguales a 2R.
