TIR de un bono
La TIR de un bono es el tipo de interés al que se deben descontar los flujos de caja que genera para que el resultado del valor actual sea igual al precio del bono.
Es decir, en términos mucho más sencillos, la TIR es la rentabilidad real que genera el bono.
Por ejemplo, si compramos un bono a 105 y nos dan un cupón anual del 5%, en realidad tendremos una rentabilidad inferior al 5%. ¿Por qué? Porque hemos pagado 105 y nos devolverán 100 (siempre nos devuelven 100). Por ello, a ese 5% anual habría que descontar el valor que nos devuelven de menos.
Al contrario, si compramos un bono a 95 y nos pagan un 5% anual, en realidad nuestra TIR será mayor de 5%. Hemos pagado 95 y nos devuelven 100, es decir, más de lo que hemos pagado. Por tanto, al 5%, habrá que añadir ese extra que nos devuelven de más. Para ello, existen unas fórmulas.
A continuación veremos cómo se calcula la TIR y al final veremos ejemplos de los tres posibles casos. Comprando un bono a la par, comprando un bono a descuento (por debajo de 100) o comprando un bono con prima de emisión (por encima de 100).
Cálculo de la TIR de un bono
La fórmula de la TIR ya se vio en otro artículo sobre la Tasa Interna de Retorno. En este caso, la fórmula es la misma, pero aplicada a la inversión en un bono. Para simplificar, podemos invertir en dos tipos de bonos:
- Bonos cupón cero: La TIR de un bono cupón cero coincide con el tipo de interés al contado. El único flujo de caja es el precio de reembolso.
- Bonos con cupones: La TIR de un bono con cupones se obtiene por prueba y error a través de una fórmula. Existen programas informáticos que nos facilitan esta tarea.
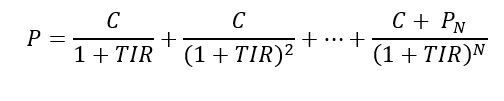
Donde P es el precio de compra del bono, Pn el precio de reembolso y C el cupón de cada periodo.
Ejemplo de cálculo de la TIR de un bono
- Supongamos un bono cupón cero, es decir, un bono que no reparte cupones. El precio de compra del bono es de 109, el plazo de vencimiento 3 años.
La TIR de este bono cupón cero es de -0,028. Si multiplicamos por 100 y lo expresamos en porcentaje nos queda que la TIR de este bono es de -2,8%. Con lo cual podemos ver que la rentabilidad de un bono también puede ser negativa.
- Ahora supongamos un bono con cupones. El bono paga un 5% anual, con vencimiento a tres años. Y vamos a tener en cuenta tres casos:
Bono comprado con descuento (por debajo de 100)
La fórmula de la hoja de cálculo arroja un valor de la TIR de un 6,9%. Para comprobar que el cálculo es correcto, al sustituir este valor en la fórmula superior se cumplirá la igualdad.
Bono comprado a la par (en 100)
Tras introducir los valores en el programa informático, la TIR es exactamente del 5%. Con lo cual, siempre que el valor de compra sea igual al precio de amortización o reembolso, la TIR será igual al cupón.
Bono comprado con prima de emisión (por encima de 100)
Por último, en los bonos con prima de emisión la TIR será menor a la rentabilidad del cupón. La hoja de cálculo extrae un valor de la TIR de 3,22%.
En el caso de los bonos con interés variable, la fórmula a aplicar sería la misma. No obstante, variaría el resultado.
