Tipos de matrices
Definir los tipos de matrices básicos es primordial para poder construir otros tipos y métodos mucho más complejos.
La base es fundamental. Y cuando hablamos de base no nos estamos refiriendo a ningún concepto matemático. Nos estamos refiriendo a la base de conocimientos. Las matrices son uno de los conceptos más importantes y ampliamente utilizados en diferentes campos de la ciencia.
En econometría, en la programación informática, en big data y en diversos campos en los que se trate de cruzar datos o se trabaje con una gran cantidad de datos.
Una matriz cuadrada cumple que (m = n). En otras palabras, tiene el mismo número de filas y columnas. Entonces, la dimensión de las filas será la misma que la dimensión de las columnas.
La matriz cuadrada es muy importante porque es la base de muchos tipos y métodos matriciales.
Ejemplo
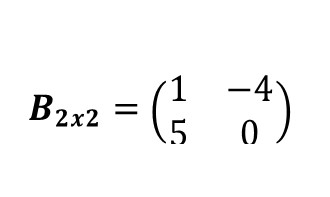
Dimensión de la matriz B = 2 x 2.
Una matriz traspuesta consiste en reordenar la matriz original cambiando las filas por columnas y las columnas por filas.
Generalmente una matriz traspuesta se indica con un superíndice T o un apóstrofe (‘). Para expresarlo mejor, optamos por el superíndice T.
Siguiendo el ejemplo anterior sería: BT.
Ejemplo

Cuando la matriz original es una matriz cuadrada, como en nuesto caso, la dimensión de la matriz sigue siendo la misma porque el número de filas y columnas es el mismo.
Dimensión de la matriz BT = 2 x2.
La matriz identidad es una matriz cuadrada la cual todos sus elementos son ceros menos los que pertenecen a su diagonal principal. Generalmente se identifica con la letra I.
La matriz identidad puede distinguirse rápidamente sin hacer ningún tipo de cálculo.

Hemos asignado una dimensión 3×3 en este caso. Sin embargo, esta dimensión puede ser más grande o más pequeña. Solo tenemos que cumplir cuando la matriz siga siendo cuadrada y cumpla con la característica: todo ceros menos su diagonal principal que debe tener unos.
Ejemplo
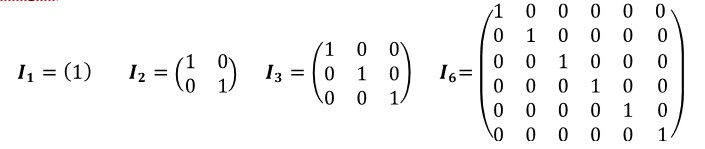
La matriz identidad actúa como el número 1 en álgebra común. Sea I la matriz identidad y B una matriz cualquiera, el producto de ambas tiene un efecto neutral sobre la matriz B. Luego, la matriz B es los mismo que IB.
Una matriz triangular es una matriz cuadrada en la cual los elementos por debajo de la diagonal principal son ceros o los elementos por encima de la diagonal principal son ceros.
La matriz triangular se centra en la localización de triángulos que contienen solo ceros. Dependiendo de su posición respecto la diagonal principal, la matriz triangular se denominará superior o inferior.
Matriz triangular superior (upper):

Matriz triangular inferior (lower):
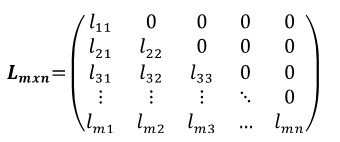
La matriz triangular participa en el método de descomposición Lower-Upper (LU) del cual se parte para obtener la descomposición de Cholesky. Este método es muy utilizado en finanzas cuantitativas para transformar variables normales independientes en variables normales correlacionadas.
Una matriz es simétrica si es una matriz cuadrada y coincide con su traspuesta (C=CT).
Para encontrar matrices simétricas de forma sencilla, solo tenemos que fijarnos en los triángulos de elementos que están por encima y por debajo de la diagonal principal.
Ejemplo
