Matriz simétrica
Una matriz simétrica es una matriz de orden n con el mismo número de filas y columnas donde su matriz traspuesta es igual a la matriz original.
En otras palabras, una matriz simétrica es una matriz cuadrada y es idéntica a la matriz de después de haber cambiado las filas por columnas y las columnas por filas.
Requisitos
Para que una matriz cualquiera sea una matriz simétrica debe cumplir las siguientes restricciones:
Dada una matriz simétrica P de orden n,
- Ser una matriz cuadrada.
El número de filas (n) tiene que ser el mismo que el número de columnas (m). Es decir, el orden de la matriz tiene que ser n dado que n=m.
- La matriz original tiene que ser igual a su matriz traspuesta.
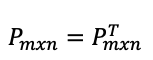
Demostración:
Propiedades
- La matriz adjunta de una matriz simétrica también es una matriz simétrica.
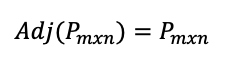
Demostración:
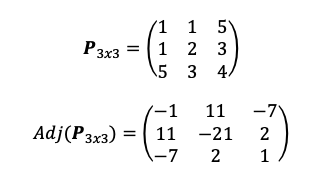
- La suma o resta de dos matrices simétricas resulta en otra matriz simétrica.
Demostración:
Dadas dos matrices simétricas P y T de orden 3, obtenemos otra matriz simétrica S a partir de la suma.
¿Por qué se llama matriz simétrica?
La propiedad de simetría viene dada por los elementos que hay alrededor de la diagonal principal. Dado que una matriz cuadrada es una matriz simétrica, siempre tendrá el mismo número de elementos por encima y por debajo de la diagonal principal. Estos elementos son iguales de forma simétrica. Es decir, la diagonal principal actúa como un espejo.
Demostración de simetría y asimetría de una matriz
Matriz simétrica
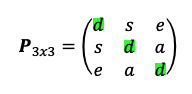
La letra d representa los elementos de la diagonal principal. Las otras letras representan cualquier número real. Podemos ver que la diagonal principal actúa como un espejo: refleja los elementos de ambos lados. En otras palabras, cuando los elementos de ambos lados de la diagonal son iguales simétricamente decimos que la matriz P es una matriz simétrica.
Matriz no simétrica
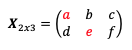
La matriz X no es una matriz simétrica dado que no es una matriz cuadrada y su matriz traspuesta es distinta a la matriz original. Además, tampoco tiene diagonal principal.
