Conjuntos numéricos
Los conjuntos numéricos son las categorías en las que se clasifican los números, en función de sus diferentes características. Por ejemplo, si tienen o no una parte decimal, o si poseen un signo negativo delante.
Los conjuntos numéricos son, en otras palabras, los tipos de números que las personas tenemos a nuestra disposición para realizar operaciones, tanto cotidianas como a un nivel más sofisticado (por parte de ingenieros o científicos, por ejemplo).
Estos conjuntos son creación de la mente humana, y forman parte de una abstracción. Es decir, no existen materialmente hablando.
A continuación, explicaremos los principales ejemplos de conjuntos numéricos, los cuales pueden verse representados en la imagen superior.
Los números naturales son aquellos que toman intervalos discretos de una unidad, y empiezan con el número 1, extendiéndose hasta el infinito. Una forma de distinguir estos números es como aquellos que sirven para contar.
En términos formales, el conjunto de números naturales se expresa con la letra N y de la siguiente forma:
Los números enteros incluyen los números naturales, más aquellos que también toman intervalos discretos, pero que tienen un signo negativo por delante, y se incluye el cero. Lo podemos expresar de la siguiente manera:
Dentro de este conjunto, cada número tiene su correspondiente opuesto con otro signo. Por ejemplo, el opuesto de 10 es -10.
Los números racionales incluyen no solo aquellos enteros, sino también los que pueden expresarse como el cociente de dos números enteros, de manera que pueden tener una parte decimal.
El conjunto de números racionales puede expresarse de la siguiente forma:
Conviene señalar que la parte decimal de un número racional puede repetirse indefinidamente, caso en el cual se le denomina periódico. Así pues, puede tratarse de un periódico puro, cuando la parte decimal contiene uno o más números que se repiten al infinito, o un periódico mixto, cuando después de la coma decimal hay algún número, o algunos números, que no se repiten, mientras que el resto sí se prolonga al infinito.
Los números irracionales no pueden expresarse como el cociente de dos números enteros, tampoco se puede especificar una parte periódica que se repita, aunque se extienden hasta al infinito.
Los números irracionales y los racionales son conjuntos disjuntos. Es decir, no tienen elementos en común.
Veamos algunos ejemplos de números irracionales:
Los números reales son aquellos que incluyen tanto a los números racionales como a los irracionales.
Es decir, los números reales van desde el menos infinito hasta el más infinito.
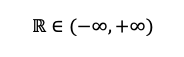
Los números imaginarios son el producto de cualquier número real por la unidad imaginaria, es decir, por la raíz cuadrada de -1.
Los números imaginarios pueden expresarse de la siguiente manera:
r = n·i
donde:
- r es un número imaginario.
- n es un número real.
- i es la unidad imaginaria.
Cabe recalcar que los números imaginarios no forman parte de los números reales.
Los números complejos son aquellos que tienen una parte real y otra imaginaria. Su estructura es la siguiente:
h + ui
Donde:
- h es un número real.
- u es la parte imaginaria.
- i es la unidad imaginaria.
