Números imaginarios

En otras palabras, los números imaginarios son números complejos y pueden escribirse como la multiplicación de la unidad imaginaria i por un número real cualquiera.

Se utiliza la i para denotar la unidad imaginaria dado que proviene del inglés, imaginary numbers. 

Dado un número imaginario r, este puede expresarse como: 

r = n·i

donde: 

• r es un número imaginario.
• n es un número real.
• i es la unidad imaginaria. 

En las operaciones matemáticas que hacemos día a día encontramos números imaginarios más veces de las que creemos. Veámoslo resolviendo la siguiente raíz cuadrada: 

¿Cuántas veces hemos estado resolviendo una ecuación cuadrática y hemos dicho que no había solución porque nos encontramos con una raíz negativa? Pues bien, esta raíz negativa, sea la que sea, se puede descomponer, tal y como se indica arriba, y llegar a tener un número real y la unidad imaginaria. En este caso, la parte real es el número 8 y la parte imaginaria es la raíz cuadrada de -1. 

La raíz cuadrada de -1 es conocida como la unidad imaginaria. 

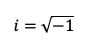
Entonces, la solución de esta raíz sería: 

Recordando la definición anterior, sabemos que un número imaginario es igual a la multiplicación de un número real cualquiera por la unidad imaginaria. Entonces:  

Los números imaginarios forman parte del conjunto de los números complejos el cual se divide entre números reales y números imaginarios. 

Parece que la idea de imaginarse números no sea muy convincente, pero realmente son de gran utilidad. Dado el anterior ejemplo, los números imaginarios dan respuesta a problemas que los números reales no pueden. 

Ahora cuando nos encontremos con una raíz negativa ya podremos solucionar el problema.

Los números imaginarios se emplean mucho en el campo de la electricidad, en la mecánica cuántica, en las transformaciones de Fourier y, combinados con números reales, crean los números complejos, muy utilizados también en el campo de las matemáticas.

A los números imaginarios se los nombró imaginarios con motivo de burla dado que eran concebidos como un conjunto numérico imposible y contrarios a los números reales.