Números reales
Los números reales son cualquier número que corresponda a un punto en la recta real y pueden clasificarse en números naturales, enteros, racionales e irracionales.
En otras palabras, cualquier número real está comprendido entre menos infinito y más infinito y podemos representarlo en la recta real.
Los números reales son todos los números que encontramos más frecuentemente dado que los números complejos no se encuentran de manera accidental, sino que tienen que buscarse expresamente.
Los números reales se representan mediante la letra R ↓
Dominio de los números reales
Entonces, tal y como hemos dicho, los números reales son los números comprendidos entre los extremos infinitos. Es decir, no incluiremos estos infinitos en el conjunto.
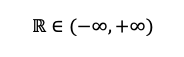
Números reales en la recta real
Esta recta recibe el nombre de recta real dado que podemos representar en ella todos los números reales.

Los números reales y la Matrioshka
Tenemos que entender el conjunto de reales como la Matrioshka, es decir, como el conjunto de muñecas tradicionales rusas organizadas de mayor a menor.
La serie de las muñecas sería tal que la muñeca más grande contiene la siguientes muñecas más pequeñas. Este conjunto de muñecas recogido dentro de la muñeca más grande se llama Matrioshka. Esquemáticamente:
(Muñeca A > Muñeca B > Muñeca C) = Matrioshka
Esquema Martioshka

La Matrioshka la podemos ver de lado (figura a la izquierda del igual) y también desde arriba o abajo (figura a la derecha del igual). De las dos formas podemos ver claramente la jerarquía de dimensiones que sigue la serie.
Entonces, de la misma manera que recogemos las muñecas rusas también podemos organizar los números reales siguiendo el mismo método.
Esquema de los números reales
En este esquema podemos ver claramente que la organización de los números reales es similar al juego de muñecas rusas visto desde arriba o abajo.
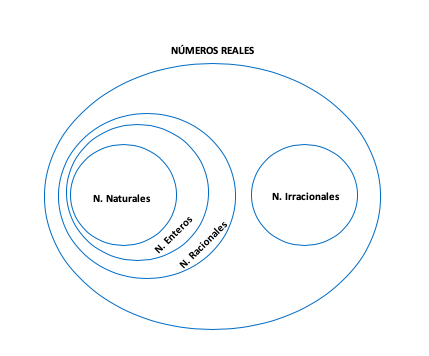
Clasificación de los números reales
Tal y como hemos visto, los números reales pueden clasificarse entre números naturales, enteros, racionales e irracionales.
Los números naturales es el primer conjunto de números que aprendemos de pequeños. Este conjunto no tiene en cuenta el número cero (0) excepto que se especifique lo contrario (cero neutral).
Expresión:
Pista → Nos podemos acordar de los números naturales pensando en que son los números que usamos “naturalmente” para contar. Cuando contamos con la mano obviamos el cero, lo mismo para los números naturales.
Primeros elementos del conjunto de números naturales.
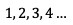
Los números enteros son todos los números naturales e incluyen el cero (0) y todos los números negativos.
Expresión:
Ejemplo de algunos de los elementos del conjunto de números enteros.
Pista: → Nos podemos acordar de los números enteros pensando en que son todos los números que usamos naturalmente para contar junto con sus opuestos e incluyendo el cero (0). A diferencia de los racionales, los números enteros representan “enteramente” su valor.
Los números racionales son las fracciones que pueden formarse a partir de los números enteros y naturales. Entendemos las fracciones como cocientes de números enteros.
Expresión:
Pista → Nos podemos acordar de los números racionales pensando en que siendo fracciones de números enteros, es “racional” que el resultado sea un número entero o un número decimal finito o semiperiódico.
Ejemplo de algunos de los elementos del conjunto de números racionales.
Los números irracionales son números decimales que no pueden expresarse ni de manera exacta ni de manera periódica.
Expresión:
Pista → Nos podemos acordar de los números irracionales pensando en que son todos los números que no encajan en las clasificaciones anteriores y que también pertenecen a la recta real.
Ejemplo de algunos elementos del conjunto de números irracionales.
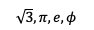
Ejemplos de números reales
En el siguiente ejemplo sobre los números reales, comprueba que los siguientes números corresponden a punto en la recta real.
- Números naturales: 1,2,3,4…
- Números enteros: …,-4,-3,-2,-1, 0, 1, 2, 3, 4…
- Números racionales: cualquier fracción de números enteros.
- Números irracionales:
