Números complejos

En otras palabras, los números complejos son números que tienen una parte real y una parte imaginaria. 

Una forma fácil de recordar cómo son los números complejos es memorizar el siguiente esquema: 

Entonces, sabiendo que dentro de los números complejos encontramos los números reales y los números imaginarios, es más fácil comprender que los números complejos son combinaciones de números reales y números imaginarios. ¡Podemos combinarlos de las formas que queramos!

Cuando pensemos en números complejos, debemos pensar en el adjetivo de “completo” más que en el adjetivo de “complicado”. Completo en el sentido que comprende ambos mundos: el real y el imaginario.  

La representación más común de un número complejo es la suma de una parte real y una parte imaginaria. Al mismo tiempo, la parte imaginaria se divide entre la parte imaginaria y la unidad imaginaria. 

Dado un número real y un número imaginario, podemos crear la siguiente combinación: 

h + ui

Donde:

• h es un número real. 
• ui es un número imaginario. 

De forma más concreta: 

• h es un número real. 
• u es la parte imaginaria. 
• i es la unidad imaginaria. 

Entonces, ¿siempre que encontremos una combinación de números y veamos una “i”, querrá decir que se trata de un número complejo? 

Esta pregunta tiene trampa porque todos los números que conocemos están comprendidos dentro del conjunto de los números complejos. Si se fijan en el esquema anterior, verán que un número real también es un número complejo. Es cierto que cuando nos encontramos un número real, no vemos ninguna “i”, este sería el caso de un número complejo donde la parte imaginaria es cero. 

Las diferentes formas de números complejos que nos podemos encontrar son las siguientes: 

	Número complejo	Número real	Número imaginario
Número complejo	h + ui	h	ui
Número complejo puramente real	h	h	0
Número complejo puramente imaginario	ui	0	ui

• Número complejo puramente real: Es un número complejo donde la parte imaginaria es 0. En otras palabras, es un número real cualquier número de menos infinito a más infinito.
• Número complejo puramente imaginario: Es un número complejo donde la parte real es 0. En otras palabras, es un número imaginario, cualquier número real que lleve al lado una “i”.  

Si bien los números complejos se escriben como combinaciones de números reales e imaginarios, su representación gráfica también seguirá el mismo patrón. 

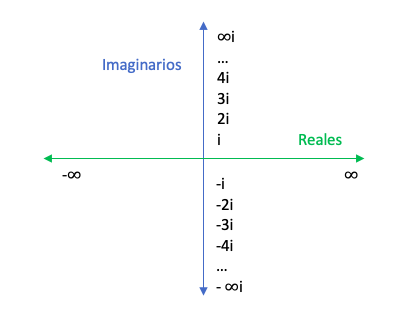
A este gráfico se le llama plano complejo porque representa tanto los números reales como los números imaginarios, en otras palabras, los números complejos. 

Los números complejos son muy utilizados en el campo de las matemáticas, sobretodo en la disciplina de los fractales. 

Pensar en ejemplos de números que puedan completar la siguiente tabla: 

	Número complejo	Número real	Número imaginario
Número complejo	3 + 4i	3	4i
Número complejo puramente real	3	3	0
Número complejo puramente imaginario	4i	0	4i

Cabe destacar, no obstante, que esta tabla se puede rellenar de otras formas y con otros números. Eso sí, siempre cumpliendo la estructura que se detalló al principio y en el que se explicaba su fórmula.