Unidad imaginaria
La unidad imaginaria es la raíz cuadrada de un número negativo que, multiplicado por un número real cualquiera forma un número imaginario y se expresa mediante una i.
En otras palabras, la unidad imaginaria es la raíz cuadrada de -1 y crea un número imaginario cuando se multiplica por un número real cualquiera.
Artículo recomendado: números imaginarios.
Fórmula de la unidad imaginaria
La unidad imaginaria se expresa de la forma:
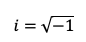
Se utiliza la “i” para denotar la unidad imaginaria dado que proviene del inglés, imaginary numbers. Como no podemos utilizar los números reales para dar solución a la ecuación anterior que parece imposible, tendremos que “imaginar” un número que sí lo hace.
Para entender de donde viene la igualdad anterior, quitaremos la raíz de la derecha del igual y elevaremos al cuadrado la i. Una vez elevada, la podemos descomponer como el producto de dos i, tal que:
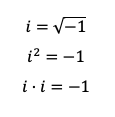
Ahora pensamos, ¿existe algún número que multiplicado por él mismo resulte en un número negativo?
Si pensamos en un número real, la respuesta es no.
Si pensamos en un número imaginario, la respuesta es sí.
Ejemplo
Aceptando la propiedad anterior, podemos resolver la siguiente ecuación:
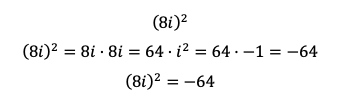
Este resultado puede reducirse para que nos sea más familiar quitando la potencia de la izquierda y añadiendo la raíz cuadrada a la derecha:
La ecuación anterior es la expresión de un número imaginario, compuesto por la parte real, número 8, y la parte imaginaria, i, es decir, la unidad imaginaria.
Propiedades de la unidad imaginaria
La unidad imaginaria posee tres propiedades.
Propiedad 1
1 · i = i
La multiplicación de 1 con la i produce un efecto neutro.
Propiedad 2
i · i = -1
-i · i = 1
Esta propiedad es la más importante dado que solo la poseen los números imaginarios.
Propiedad 3
-1 · i = -i
La multiplicación de -1 con la i produce un cambio de signo en la i.
Aplicación
Dado que la unidad imaginaria forma parte de los números imaginarios, su utilización es muy práctica para dar solución a problemas matemáticos que no pueden solucionarse mediante números reales.
