Ángulo entre dos vectores
El ángulo entre dos vectores es la capacidad del arco de la circunferencia que forman los segmentos de los vectores unidos por un punto.
En otras palabras, el ángulo entre dos vectores es el ángulo que se forma cuando dos vectores se multiplican.
Dos vectores formarán un ángulo cuando ambos se estén multiplicando, es decir, cuando multipliquemos vectores los estaremos uniendo en un punto en común tal que formarán un ángulo.
Fórmula
Sean dos vectores de 3 dimensiones:
Ambos formaran un ángulo si hacemos el producto escalar:
Fórmula del producto escalar
El proceso de pasar de dos vectores a tener un ángulo sería el siguiente:
Para obtener el ángulo que se forma del producto escalar de dos vectores se debería aislar el coseno y luego hacer el arcoseno y encontrar alpha (el ángulo).
Entonces, el procedimiento a seguir sería: primero, escribir la fórmula del producto escalar en definición geométrica porque queremos que la multiplicación incorpore el coseno.
Después, aislar el coseno del ángulo a través de pasar dividiendo el producto de los módulos de los vectores al otro lado del igual.
Es importante diferenciar que el producto escalar en coordenadas (numerador) es diferente que el producto de los módulos (denominador).
El producto escalar en coordenadas es:
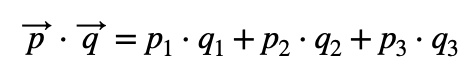
El producto de los módulos es:
Tipo de ángulos según el signo del producto escalar
El signo del producto escalar de dos vectores determinará el ángulo que se forma y con él también su forma:
- Si el producto escalar es positivo, entonces, el ángulo que se forma es agudo.
- Si el producto escalar es cero, entonces, el ángulo que se forma es recto. Cuando se forma un ángulo recto quiere decir que los vectores son perpendiculares.
- Si el producto escalar es negativo, entonces, el ángulo que se forma es obtuso.
