Producto escalar de vectores con definición geométrica
El producto escalar de dos vectores según su definición geométrica es la multiplicación de sus módulos por el coseno del ángulo que forman ambos vectores.
En otras palabras, el producto escalar de dos vectores es hacer el producto de los módulos de ambos vectores y el coseno del ángulo.
Fórmula del producto escalar
Dados dos vectores, el producto escalar se calcula de la siguiente forma:
Se llama producto escalar porque el resultado del módulo siempre será un escalar, de la misma forma que también lo será el coseno de un ángulo. El resultado de esta multiplicación será un número que expresa una magnitud y no tiene dirección. En otras palabras, el resultado del producto escalar será un número, no un vector. Por tanto, el número resultante lo expresaremos como un número cualquiera y no como un vector.
Para saber la magnitud de cada vector se calcula el módulo. Entonces, si multiplicamos la magnitud de uno de los vectores (v) por la magnitud del otro vector (a) por el coseno del ángulo que forman ambos, sabremos cuánto miden los dos vectores en total.
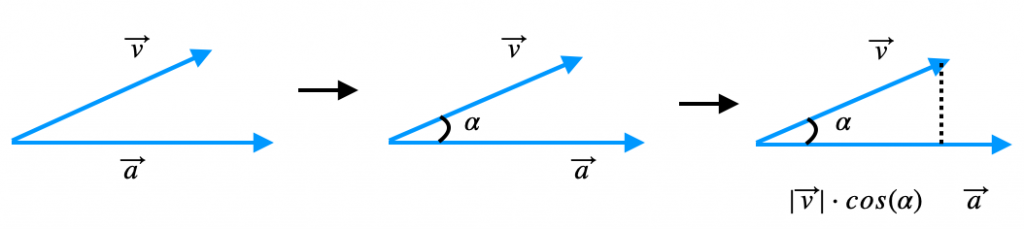
El módulo del vector ( v) por el coseno del ángulo también se conoce como la proyección del vector v sobre el vector a.
Procedimiento
- Calcular los módulos de los vectores.
Dado un vector cualquiera de tres dimensiones,
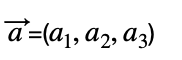
La fórmula para calcular el módulo de un vector es:
Cada subíndice del vector indica las dimensiones, en este caso, el vector (a) es un vector de tres dimensiones porque tiene tres coordenadas.
2. Calcular el coseno del ángulo.
Ejemplo del producto escalar de dos vectores
Calcula el producto escalar de los siguientes vectores de tres dimensiones conociendo que el ángulo que forman es 45 grados.
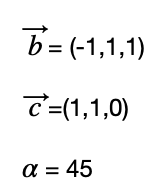
Para calcular el producto escalar primero tenemos que calcular el módulo de los vectores:
Una vez hemos calculado los módulos de los dos vectores y conocemos el ángulo, solo falta multiplicarlos:
Por tanto, el producto escalar de los vectores anteriores es de 1,7320 unidades.
Gráfica
El aspecto que tendrían los siguientes vectores en un gráfico de tres dimensiones sería el siguiente:
Para el vector (c) podemos ver que la componente z es cero, por tanto, será paralelo al eje de las abscisas. En cambio, la componente z del vector (b) es positiva, por tanto, podemos ver cómo se inclina hacia arriba. Ambos vectores están en el cuadrante de los positivos en cuanto a la componente, dado que es positiva y es la misma.
