Producto escalar de dos vectores
El producto escalar de dos vectores en coordenadas es el sumatorio del producto de las coordenadas de cada vector conservando el orden de las dimensiones.
En otras palabras, el producto escalar en coordenadas de dos vectores es el resultado de multiplicar las coordenadas de la misma dimensión de los vectores y sumarlas.
Se llama producto escalar porque el resultado de la multiplicación siempre será un escalar. El resultado de esta multiplicación será un número que expresa una magnitud y no tiene dirección. En otras palabras, el resultado del producto escalar será un número, no un vector. Por tanto, el número resultante lo expresaremos como un número cualquiera y no como un vector.
Para expresar el producto de vectores en coordenadas se emplea el sistema de referencia canónico.
En este artículo veremos, todo sea dicho, dos formas de calcular el producto escalar de dos vectores. El primero se ha descrito anteriormente, mientras que el segundo lo veremos más tarde.
Fórmula del producto de dos vectores
Dados dos vectores:
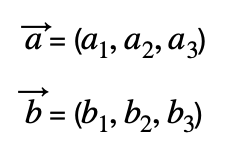
El producto escalar se calcula de la siguiente forma:
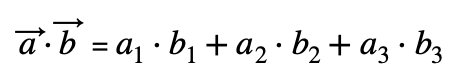
El producto escalar de dos vectores se obtiene a través de multiplicar las coordenadas de los vectores siempre conservando las dimensiones. En otras palabras, solo se pueden multiplicar las coordenadas de la misma dimensión.
En el primer ejemplo está bien porque estamos multiplicando la primera coordenada del vector a y del vector b. El segundo ejemplo está mal porque estamos multiplicando la primera coordenada del vector a y la segunda coordenada del vector b. Multiplicar coordenadas de distinta dimensión no es correcto.
Fórmula del producto escalar para k vectores
Dados k vectores con n coordenadas:
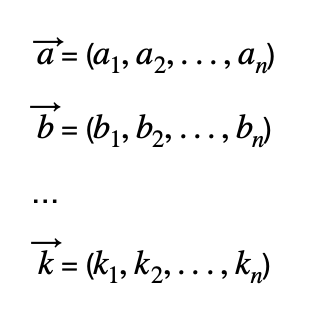
El producto escalar se calcula de la siguiente forma:
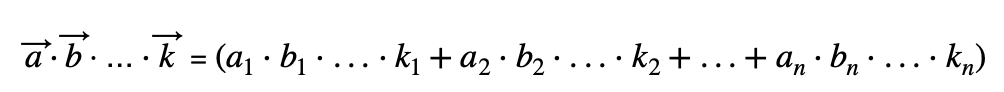
Aunque tengamos muchos vectores con muchas dimensiones, el producto escalar funciona de la misma forma: hacer la suma de la multiplicación de las coordenadas que sean de la misma dimensión.
Pasos a seguir para calcular el producto escalar de dos vectores
- Identificar los vectores que queremos multiplicar y sus coordenadas.
- Multiplicar las coordenadas de la misma dimensión.
- Sumar las multiplicaciones anteriores.
- Comprobar que el resultado es un único número.
Producto escalar definición geométrica
El producto escalar de dos vectores también se puede expresar cómo el producto de los módulos de ambos vectores y el coseno del ángulo de los vectores.
Dados dos vectores, el producto escalar se calcula de la siguiente forma:
Para ahondar más en esta otra forma de cálculo te recomendamos que visites el siguiente artículo:
Ejemplo del producto escalar
Calcula el producto escalar de los siguientes vectores:

El resultado de un producto escalar siempre será un escalar, es decir, un número. El resultado de nuestro ejemplo coincide con la teoría y, por tanto, es correcto.
