Módulo de un vector
El módulo de un vector es la longitud de un segmento orientado en un espacio que está determinado por dos puntos y el orden de estos.
En otras palabras, el módulo de un vector es la longitud entre el inicio y el final del vector, es decir, dónde empieza y dónde termina la flecha. Visto de otra forma, podemos decir que el módulo de un vector es lo mismo que la longitud de un vector.
Podemos entender el módulo como la distancia entre dos objetos. La distancia tiene la propiedad de ser siempre positiva. Por ejemplo, de nuestro ordenador a nosotros mismos hay una distancia. Pero esta distancia es la misma si lo miramos desde nosotros mismos hacia nuestro ordenador. Entones será cualquier número real positivo incluyendo el 0.
Fórmula del módulo de un vector de dos dimensiones
Dado un vector v de dos dimensiones con coordenadas (v1,v2), el módulo sería tal que:
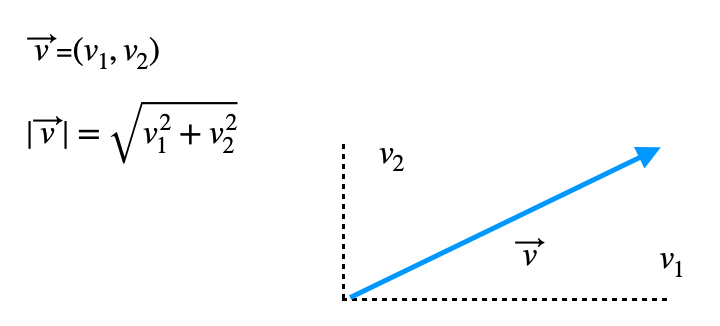
Fórmula del módulo de un vector de tres dimensiones
Dado un vector v de tres dimensiones con coordenadas (v1,v2,v3), el módulo sería tal que:
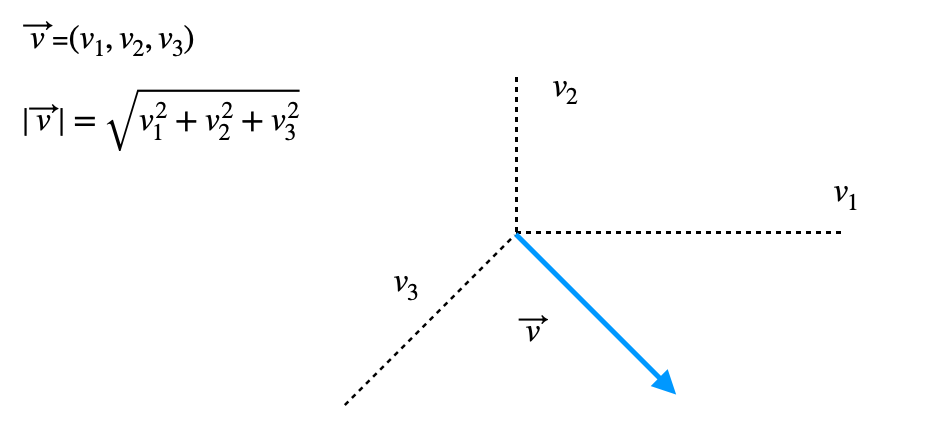
La única diferencia entre el cálculo del módulo para un vector de dos dimensiones y el cálculo del módulo de un vector de tres dimensiones es que el tercer término no aparece en la primera ecuación.
Un vector puede extenderse hasta n dimensiones. Entonces, eso quiere decir que su módulo también. Por tanto, podemos calcular y representar un vector de n dimensiones.
Representar cualquier figura en un espacio de más de tres dimensiones implica tener un buen programa gráfico. Desde el punto de vista de cálculo, es relativamente fácil calcular el módulo de un vector con 6 coordenadas, por ejemplo.
También es común expresar la fórmula del módulo en las variables de los ejes, por tanto, podemos expresar las ecuaciones anteriores de la forma:

Siendo la primera letra x, seguida de y y z.
Propiedades del módulo de un vector
Las propiedades del módulo de un vector las podemos explicar a partir de dos vectores a y v cualquiera:
- El módulo de la suma de dos vectores incluye el producto escalar.
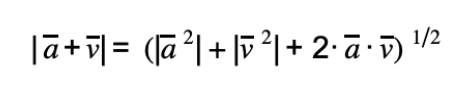
El producto escalar lo encontramos al final de la fórmula, después de la multiplicación del número dos, hay dos vectores multiplicándose. La multiplicación de dos vectores o producto escalar no se soluciona tan solo multiplicando sus módulos, sino que también se tiene en cuenta la proyección de un vector sobre el otro desde el punto de vista geométrico.
- Desigualdad triangular.
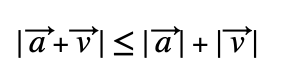
El módulo de la suma de dos vectores será siempre menor o igual que la suma individual de sus módulos.
Ejemplo del módulo de un vector
Calcula el módulo de un vector v con coordenadas (3,-4,6).
El primer paso sería escribir el vector dado y la fórmula del módulo.

