Vectores perpendiculares
Los vectores perpendiculares en el plano son dos vectores que forman un ángulo de 90 grados y su producto escalar es cero.
En otras palabras, dos vectores serán perpendiculares cuando formen un ángulo recto y, por tanto, su producto escalar será cero.
Para calcular si un vector es perpendicular a otro podemos emplear la fórmula del producto escalar desde el punto de vista geométrico. Esto es, teniendo en cuenta que el coseno del ángulo que forman será cero. Por tanto, para conocer qué vector es perpendicular a otro, solo tendríamos que igualar a 0 el producto escalar y encontrar las coordenadas del misterioso vector perpendicular.
Fórmula de dos vectores perpendiculares
La idea principal de la perpendicularidad de dos vectores es que su producto escalar sea 0.
Tal que dados 2 vectores perpendiculares cualesquiera, su producto escalar será:

La expresión se lee: “el vector a es perpendicular al vector b”.
Podemos expresar la fórmula anterior en coordenadas:
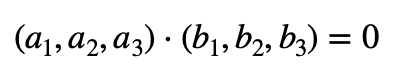
Gráfico de dos vectores perpendiculares
Los vectores anteriores representados en un plano tendrían la siguiente forma:
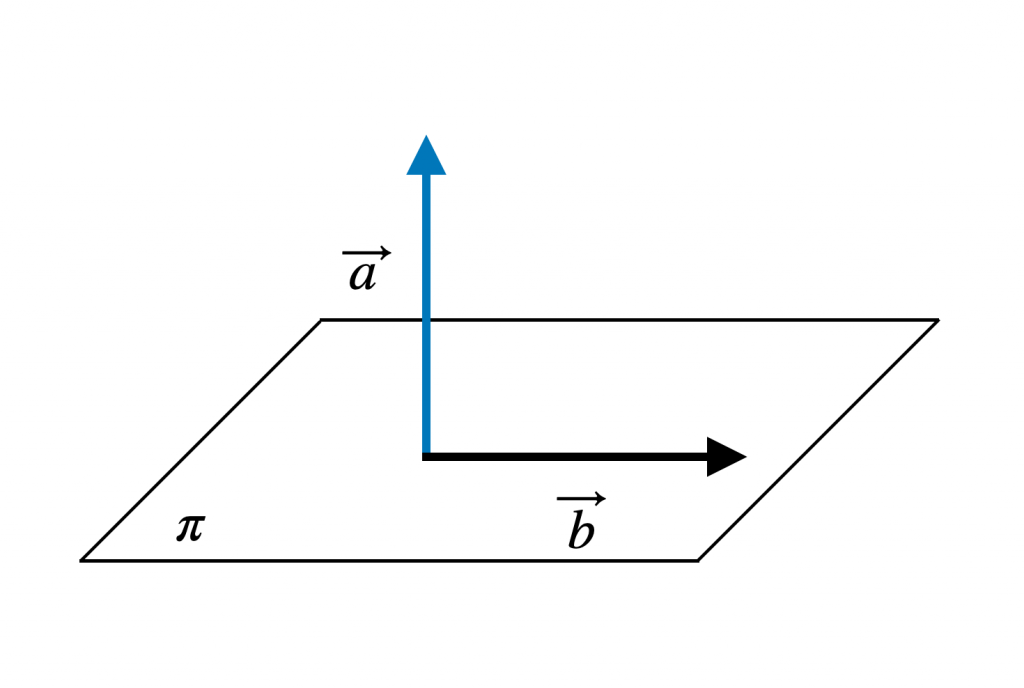
Donde podemos extraer la siguiente información:

El vector perpendicular al plano se lo conoce como vector normal y se indica con una n, tal que:
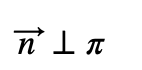
Demostración
Podemos demostrar la condición de que el producto de dos vectores perpendiculares es cero con unos pocos pasos. Por lo tanto, solo tenemos que recordar la fórmula del producto escalar desde el punto de vista geométrico.
- Escribir la fórmula del producto escalar desde el punto de vista geométrico:
2. Sabemos que dos vectores perpendiculares forman un ángulo de 90 grados. Entonces, alpha = 90, tal que así:
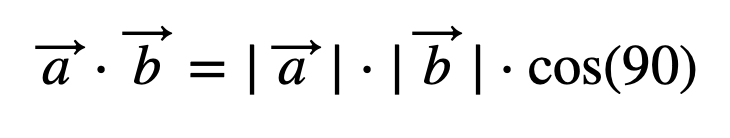
3. A continuación, calculamos el coseno de 90:
4. Vemos que al hacer la multiplicación del coseno de 90 con el producto de los módulos, se elimina todo porque se están multiplicando por 0.
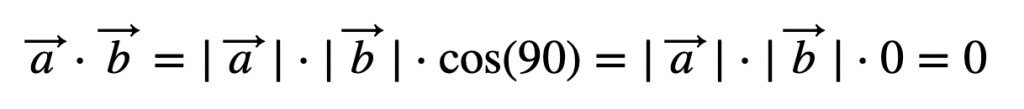
5. Finalmente la condición será:
Ejemplo
Expresa la ecuación en función de un vector cualquiera que sea perpendicular al vector v.
Para hacer esto definimos un vector p cualquiera y dejamos como incógnitas sus coordenadas dado que nos las conocemos.
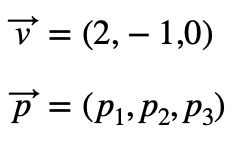
Entonces, aplicamos la fórmula del producto escalar:
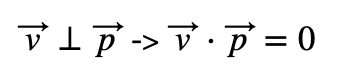
Finalmente, expresamos el producto escalar en coordenadas:
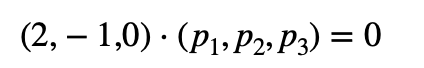
Resolvemos la ecuación anterior:
Entonces, esta sería la ecuación en función del vector p que sería perpendicular al vector v.
.
