Definición de polígono cóncavo
Aquellas figuras de la geometría que son planas y que están formadas por segmentos rectos y no alineados reciben el nombre de polígonos. Dentro de esta clasificación, es posible encontrar una gran cantidad de variedades que dependen de las características que se analicen.
Los polígonos cóncavos, en este sentido, son las figuras de este tipo que tienen uno o más ángulos interiores que miden más de pi radianes o de 180°. Estos polígonos, por otra parte, disponen de una o más diagonales que resultan exteriores.
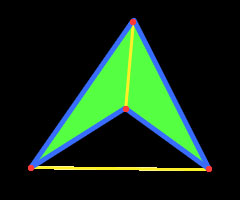
La diagonal del polígono se define como la unión de dos vértices no consecutivos de la figura. En este caso, como se puede apreciar en la segunda imagen, uno de los segmentos comprendidos entre dos puntos no consecutivos se encuentra fuera del polígono, y por eso se habla de diagonal exterior, algo que caracteriza a los polígonos cóncavos. Como es de esperarse, este rasgo complica ciertos cálculos, como ser su superficie, especialmente en el ámbito de las aplicaciones interactivas por ordenador tales como los videojuegos.
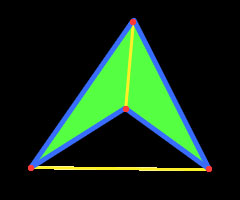
A simple vista, el polígono cóncavo puede parecer una figura extremadamente compleja de analizar; lo mismo ocurre con los dos que se muestran en las imágenes de este artículo. Sin embargo, tras inspeccionarlos un poco, notamos que pueden ser descompuestos en dos o más figuras geométrica convexas, y entonces los cálculos comienzan a volverse más sencillos.
Tomemos el polígono de la primera imagen, por ejemplo: con poco esfuerzo, podemos dividirlo en tres triángulos. Habiendo hecho esto, es posible calcular la superficie de cada uno aplicando uno de los siguientes métodos, según las necesidades:
* el área de todo triángulo se puede obtener multiplicando su base (cualquiera de sus segmentos, que se obtienen uniendo dos de sus vértices) por su altura (la distancia entre el punto medio de la base y el vértice restante) y luego dividiendo el resultado por 2;
* si bien la fórmula anterior también sirve para los triángulos rectángulos (aquellos que poseen un ángulo de 90° entre dos de sus lados), la manera de entenderla en este caso es multiplicando sus catetos (cada uno de los lados que forman el ángulo recto antes mencionado) entre sí y dividiendo por 2;
* los triángulos equiláteros (que poseen lados de igual extensión entre sí) presentan un desafío ligeramente mayor, dado que su superficie se calcula multiplicando su altura al cuadrado por la raíz cuadrada de 3, sobre 2.
Existen más caminos para precisar la superficie de un triángulo, pero también es posible hallar cuadrados dentro de un polígono cóncavo, algo que facilita aún más las cosas, ya que en tal caso simplemente se debe multiplicar su lado menor por el mayor. Una vez que se han calculado todas las superficies, basta sumarlas para obtener la del polígono.
Otra característica de los polígonos cóncavos es que siempre tienen dos o más vértices que, vinculados por un segmento, éste intersecará al menos uno de los lados de la figura.
Debido a estas propiedades, los triángulos (que son polígonos que tienen tres lados) nunca pueden ser cóncavos ya que sus ángulos interiores no superan nunca los pi radianes o los 180°.
El ejemplo más frecuente de los polígonos cóncavos son los polígonos estrellados, que tienen forma de estrella. Como se puede confirmar al analizar esta clase de polígonos, tienen al menos un ángulo interno con más de 180° y una diagonal exterior.
Cuando estas propiedades no se cumplen y las figuras no pueden ser clasificadas dentro del grupo de los polígonos cóncavos, ingresan en el conjunto de los polígonos convexos.
Por oposición a los polígonos cóncavos, por lo tanto, se puede definir a los polígonos convexos como aquellos con ángulos internos que no miden más de 180° o pi radianes y con diagonales que siempre son interiores.