En qué situaciones se observan las funciones lineales y cuadráticas

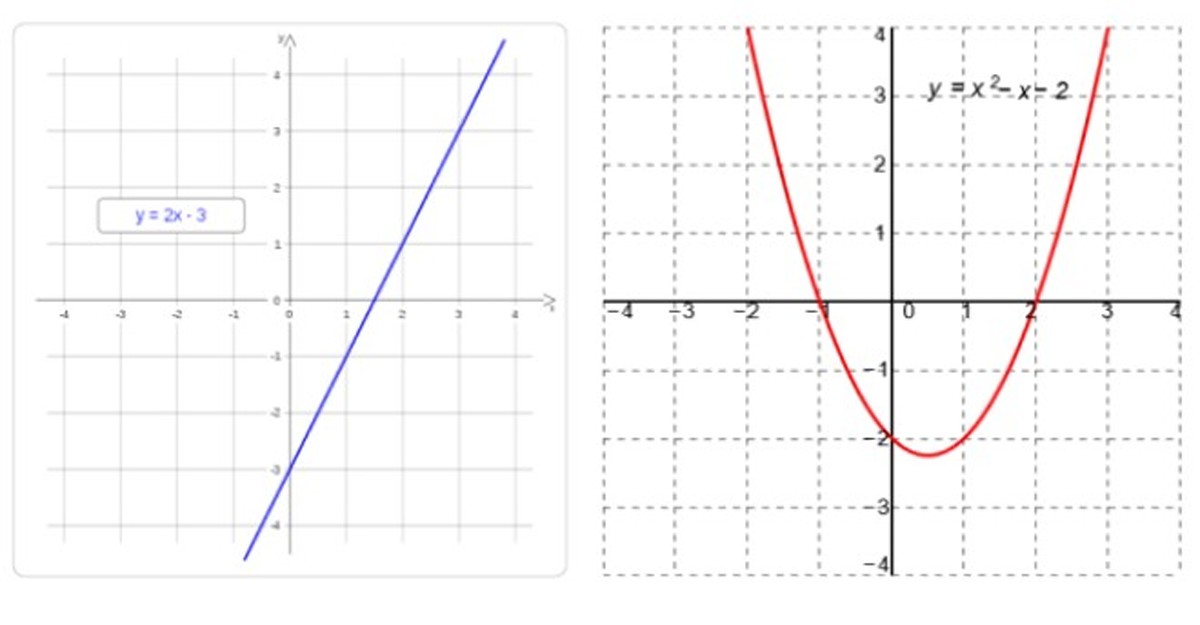
¿Qué son las funciones lineales y cuadráticas?

Las funciones lineales y las funciones cuadráticas son funciones que pertenecen al grupo de funciones polinómicas. Se utilizan para modelar diversas situaciones, como la dependencia entre el volumen y el peso de un cuerpo, la cantidad y el coste de un producto, la posición versus el tiempo y más.

En general, una función es una relación que vincula dos variables y que se puede utilizar para modelar el mundo real. Las funciones polinómicas, como su nombre lo indica, se expresan a través de un polinomio, cuya forma general es:

f(x) = a_nxⁿ + a _n-1x ^n-1 + a_x-2x^n-2 + … a_o

Donde n es un número natural, los números a₀, a₁, a₂, … a_n son reales, a₀ es el término independiente y a_n, es el coeficiente que acompaña la potencia más alta. El valor de n indica el tipo de función, para n=1 la función es lineal, mientras que para n=2 la función es cuadrática.

En el primero de estos casos, la expresión general se reduce a:

f(x) = a₁x + a_o

Y en el segundo caso, queda así:

f(x) = a₂x² + a₁x + a_o ;   (a₂≠0)

Las gráficas de las funcionespolinómicas son continuas, es decir, no experimentan saltos abruptos ni rupturas, teniendo por tanto un comportamiento suave, sin irregularidades. Por ello se observan en el modelado de multitud de situaciones de la ciencia, la economía y otras áreas del conocimiento humano.

A continuación, se describen con mayor detalle interesantes aplicaciones de unas y otras.

Situaciones en que aparecen las funciones lineales

La función lineal se representa algebraicamente mediante:

f(x) = a₁x + a_o

O equivalentemente:

f(x) = mx + b

Su característica distintiva es que su gráfica es una línea recta. El valor m, que es el coeficiente de la x, representa la pendiente de dicha recta y da una medida de cuán inclinada es.

La pendiente puede ser positiva, negativa o cero, pero siempre es constante, esto es, su tasa de cambio se mantiene inalterada.

Una recta de pendiente 0 es totalmente horizontal, la de pendiente positiva señala elevación o aumento (si una de las variables aumenta, la otra también, siempre al mismo ritmo) y, por último, la de pendiente negativa indica descenso (a medida que una de las variables aumenta, la otra disminuye).

El valor de b, por su parte, representa el corte o intersección de la recta con el eje vertical. Si b=0, la recta pasa por el origen del sistema de coordenadas.

Ejemplos de modelado con funciones lineales

1. El movimiento rectilíneo uniforme

La ecuación que vincula la posición x y el tiempo t de un móvil, en el movimiento rectilíneo uniforme, es lineal:

x(t) = v⋅t + x_o

Donde v, la pendiente de la recta, es la velocidad del móvil, la cual permanece constante a lo largo de todo el movimiento, y x_o es la posición inicial.

2. Densidad

Densidad de un objeto o de una sustancia, que establece la relación entre la masa y el volumen. Llamando ρ a la densidad (se lee “rho”), m a la masa y V al volumen, se tiene:

Despejando la masa, en términos del volumen, se obtiene:

m = ρV

Al graficar la masa en función del volumen, se obtiene una línea recta cuya pendiente es la densidad del objeto o la sustancia.

3. Longitud de una circunferencia

El contorno de una circunferencia, o longitud de la misma, es proporcional a su radio. Esto significa que cuanto mayor el radio, mayor contorno tendrá la circunferencia, de acuerdo a la ecuación:

C = 2πR

Donde C es el contorno o longitud, R es el radio y π (se lee “pi”) es una constante cuyo valor aproximado es π≈3.14…

4. Costo de enviar un paquete

Como es fácil deducir, cuanto más pesado o voluminoso es un paquete más costoso es transportarlo. Las compañías que se dedican al transporte de carga modelan sus precios siguiendo ciertas reglas, por ejemplo:

C(x) = 2.75x

En esta ecuación, C(x) es el costo en dólares de enviar un paquete cuyo peso es x libras. El valor constante 2.75 tiene unidades de dólar/libra (costo unitario).

Situaciones en que aparecen las funciones cuadráticas

Algebraicamente, una función cuadrática se representa mediante:

f(x) = a₂ x² + a₁ x + a_o

Con la condición de que el coeficiente a₂ sea distinto de 0. Se caracteriza por su gráfica en forma de parábola, cuyo eje axial o eje de simetría es vertical (paralelo al eje y).

La intersección entre la parábola y dicho eje es un punto llamado vértice. Si la parábola abre hacia arriba (a₂ > 0), el vértice es su punto mínimo, y si abre hacia abajo (a₂ 0), es el máximo.

Sobre el eje de simetría se encuentra el foco, un punto especial que determina la curvatura de la parábola. Si se hace incidir la luz del sol sobre un espejo parabólico, los rayos se reflejarán sobre la superficie, coincidiendo en el foco, que se calienta de inmediato.

Ejemplos de modelado con funciones cuadráticas

1. Altura de un proyectil lanzado verticalmente hacia arriba

Un proyectil es cualquier objeto al que se le proporciona una velocidad inicial y luego se deja en libertad, bajo la acción de la gravedad. Si la velocidad inicial es vertical, de magnitud v₀ y dirigida hacia arriba, el objeto subirá hasta una altura máxima y luego descenderá.

La ecuación de la altura h en función del tiempo t es:

h(t)= −4.9 t²+v₀ t

Donde el sentido vertical hacia arriba se toma como positivo, y el vertical hacia abajo negativo.

2. La trayectoria de un proyectil horizontal u oblicuo

Si a un proyectil se le proporciona una velocidad inicial horizontal u oblicua, describirá una trayectoria parabólica, la cual puede representarse a través de una función cuadrática como la descrita previamente.

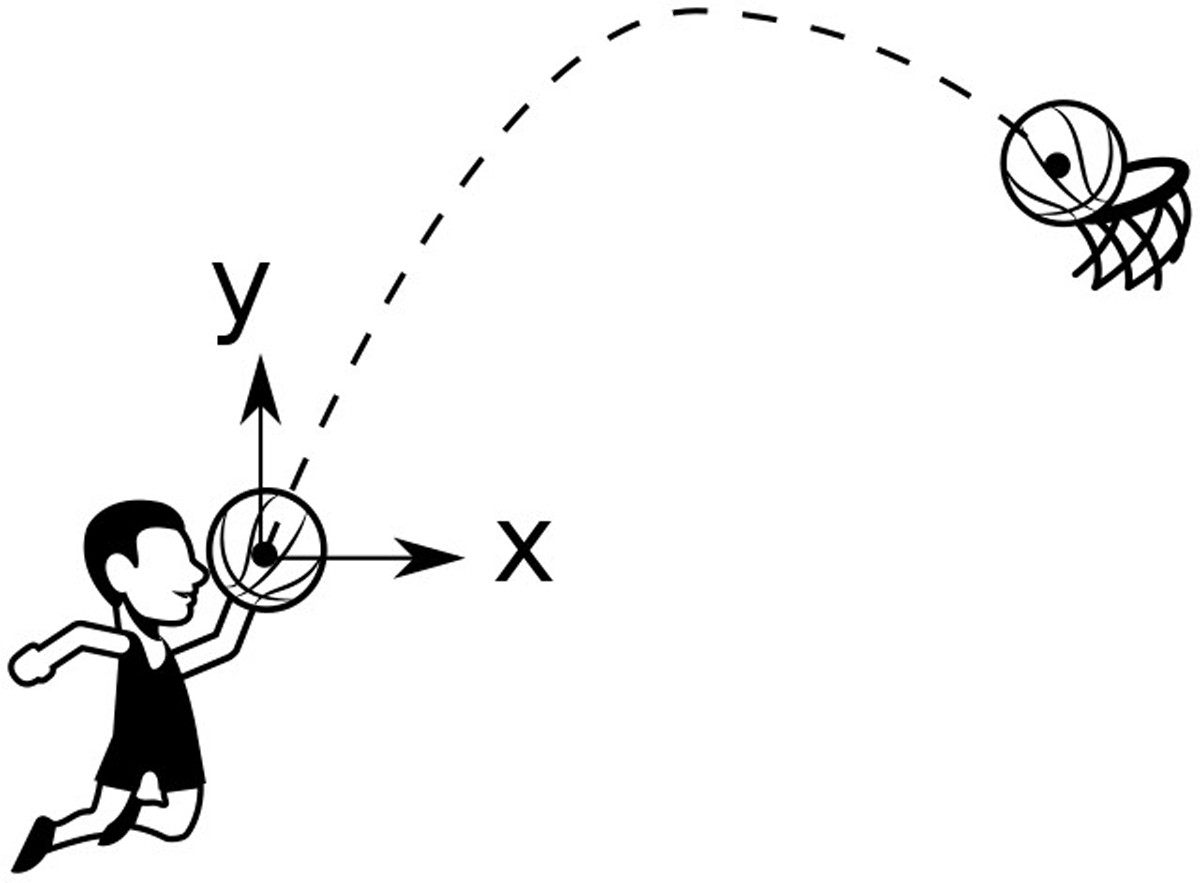
Por ejemplo, un balón lanzado desde una altura y₀, formando ángulo θ₀ respecto a la horizontal, tiene una trayectoria dada por:

Con g como la aceleración de la gravedad, la cual puede aproximarse a 10 m/s². Por ejemplo, un balón de fútbol pateado desde el suelo (y₀ = 0), con velocidad inicial de 6 m/s y ángulo de 45º respecto a la horizontal, tendrá una trayectoria dada por la siguiente parábola:

3. El área de un círculo

Cuanto mayor sea el radio del círculo, mayor será su área. En efecto, el área del círculo es proporcional al cuadrado del radio R, siendo la constante de proporcionalidad el número π:

A=πR²

4. Efectividad de un anuncio publicitario

Cuanto más lo ven, más efectivo es un anuncio comercial. La efectividad E, en una escala del 0 al 10, de un aviso se puede modelar de acuerdo a la siguiente función cuadrática:

Referencias 

1. Funciones Polinómicas. Recuperado de recursostic.educacion.es.
2. Larson, R. (2012). Precálculo. 8va. edición. Cengage Learning.
3. Miller, C. (2013). Matemática: Razonamiento y Aplicaciones. 12va. edición. Pearson Educación.
4. Stewart, J. (2012). Precálculo. Matemáticas para el Cálculo. 6ta. edición. Cengage Learning.
5. Zill, D. (2008). Precálculo con avances de Cálculo. 4ta. edición. McGraw Hill.