Volumen: concepto, fórmulas, calculo, ejemplos, ejercicios

¿Qué es el volumen?

El volumen de un cuerpo es el valor numérico que mide la cantidad de espacio ocupada por él. El alto, el ancho y la profundidad determinan el volumen, cuanto más grandes sean, mayor es el espacio ocupado.

El concepto de volumen tiene gran importancia, puesto que el mundo es tridimensional y todos los objetos tienen anchura, altura y profundidad, por lo tanto poseen volumen. Las personas lo usan con frecuencia, por ejemplo al estimar si el mueble que quieren comprar cabe en su sala o si entran en una determinada talla de vestido.

En ciertas áreas de la ciencia y la ingeniería, como por ejemplo cuando se trabaja con fluidos, sean líquidos o gases, el volumen ocupado adquiere una gran importancia: al llenar recipientes y bombear líquidos como el agua, o en el diseño de un barco para asegurarse de que no se hunda. Todo ello hace que sea imprescindible determinarlo para multitud de procesos.

Existen fórmulas para calcular el volumen de cuerpos geométricos de formas regulares, como prismas, esferas, cilindros y conos, por ejemplo, en función de algunas de sus dimensiones. Y también hay maneras de averiguar el volumen de objetos irregulares, como se describirá un poco más adelante.

Fórmulas del volumen en figuras geométricas

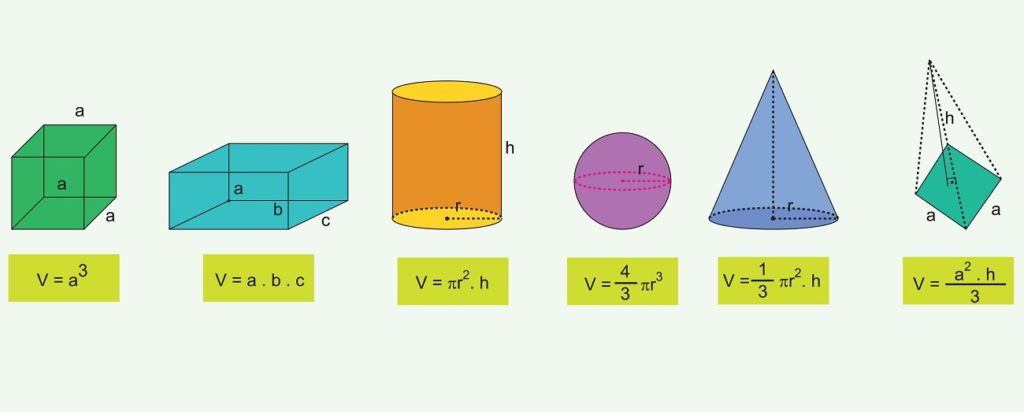
Para los objetos geométricos más conocidos existen fórmulas que permiten calcular su volumen:

• Cubo

V = ℓ³ 

Donde V representa el volumen y ℓ es la arista (lado) del cubo.

• Paralelepípedo

Un paralelepípedo es una caja rectangular con ancho “a”, largo ℓ y altura “h”. Su volumen viene dado por el producto de sus tres dimensiones:

V = a∙ℓ∙h

• Esfera

El volumen de la esfera depende de su radio r:

• Cilindro circular recto

El volumen del cilindro circular recto es el producto entre el área de su base y su altura “h”. Como la base es un disco de radio “r”, cuya área es A = π·r², el volumen queda:

V = πr²∙h

• Cono

El volumen del cono es un tercio del producto entre el área de la base circular A y la altura h. Como A = πr², entonces:

• Pirámide

Para una pirámide cuya área de la base es A y tiene una altura “h”, el volumen viene dado por:

Si la pirámide tiene base cuadrada de lado “a”, como en la figura, el área A de la base es a² y el volumen de la pirámide es:

V = (1/3)⋅a²⋅h

• Prisma

El volumen del prisma es el producto entre el área de la base A y la altura “h”:

V = A∙h

Unidades de volumen

En el Sistema Internacional de Unidades SI, la unidad para el volumen es el metro cúbico o m³, mientras que en el sistema anglosajón es el pie cúbico o ft³ (de feet, que en inglés significa “pie”).

Existen muchísimas otras unidades, de acuerdo al tamaño del espacio ocupado. Por ejemplo, los kilómetros cúbicos km³ para volúmenes mayores o los milímetros cúbicos mm³ para volúmenes pequeños. También hay unidades de uso local.

Hay que mencionar también las unidades de capacidad, estrechamente relacionadas con las de volumen, que se usan preferentemente para líquidos. La unidad central de capacidad es el litro, abreviado L, que equivale a un dm³ (decímetro cúbico).

Otras unidades que vale la pena mencionar son el galón, la pulgada cúbica, la taza y la gota, esta última muy empleada para dosificar medicamentos.

¿Cómo se mide el volumen?

El volumen de un cuerpo, al igual que cualquier otra medida, se lleva a cabo comparando con un patrón adecuado, en este caso una unidad de volumen.

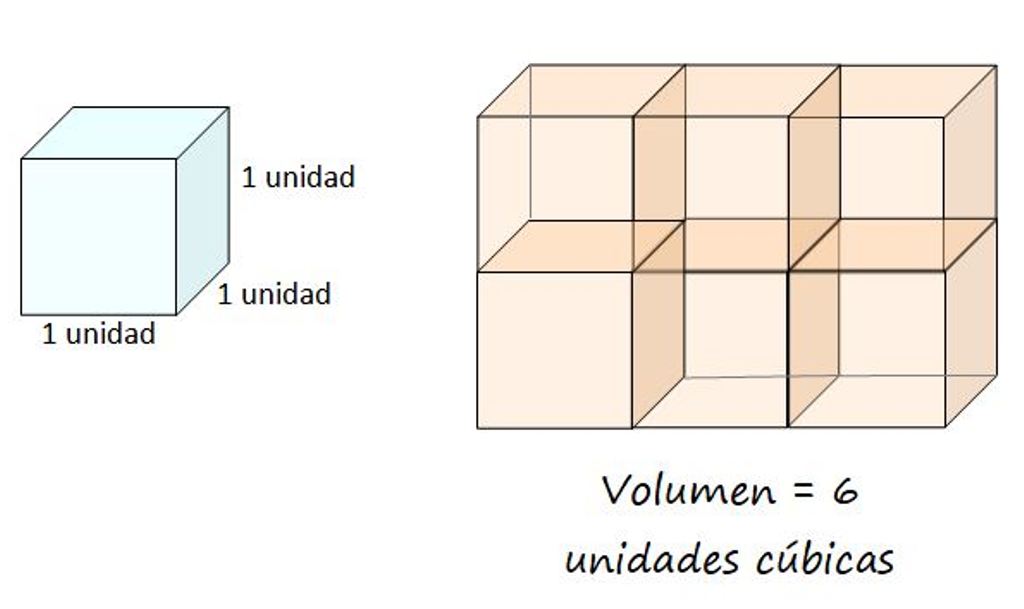
La unidad de volumen se define como la del cubo cuya arista mide 1 unidad. Esta unidad puede ser metro, centímetro, pie, pulgada o cualquier otra. Entonces, el volumen del objeto corresponde a la cantidad de unidades cúbicas ocupadas por la figura y siempre es una cantidad positiva.

Volumen de un cuerpo geométrico

Cuando se trata de un cuerpo geométrico como los ya mencionados, el volumen se calcula a través de la fórmula adecuada, midiendo las dimensiones indicadas por la fórmula.

Por ejemplo, si se quiere conocer el volumen de una esfera, es necesario medir su diámetro y con ello se conoce su radio, que es la mitad. Si se trata de una caja rectangular, se mide el ancho, la altura y la profundidad de la misma.

Luego se insertan los valores pedidos en la fórmula, cuidando que todas las unidades sean las mismas, se llevan a cabo las operaciones requeridas y listo, se tiene el volumen del objeto.

Volumen de un cuerpo irregular

Los sólidos irregulares no tienen una forma geométrica, como una piedra o un guijarro. Aun así se puede encontrar su volumen con la ayuda de un recipiente graduado lleno con agua, mediante el método de desplazamiento de líquido.

En primer lugar se determina el volumen ocupado por el agua y seguidamente se sumerge completamente el objeto irregular, midiendo el nuevo volumen, el cual es mayor que el original. El volumen del objeto irregular es la diferencia entre este volumen y el del agua sola.

Para que este método funcione, el objeto no debe estar hecho de alguna sustancia que se disuelva en el agua fácilmente, debe permanecer completamente sumergido y desde luego, hay que contar con un recipiente graduado del tamaño necesario para alojarlo completamente.

Ejemplos de volumen

El volumen aproximado de algunos objetos conocidos es:

• La Tierra: 1,08321×10¹² km³​
• Río Amazonas: 225.000 m³/s (Al volumen por unidad de tiempo se le denomina “caudal”)
• La Gran Pirámide de Giza: 2.600.000 m³
• Un balón de fútbol: 5600 cm³
• Una mochila: 50 dm³

Volumen y masa

El volumen y la masa no son sinónimos, el primero se vincula a las dimensiones del objeto y la segundo a la cantidad de materia que contiene.

Puede haber mucha materia en un objeto de pequeñas dimensiones, o muy poca en un objeto grande, lo cual depende de la densidad del material, que es el cociente entre la masa y el volumen de un objeto:

Ejercicios resueltos

Ejercicio 1

Calcular el volumen de una caja rectangular cuyas dimensiones son 34 cm × 22 cm× 8 cm.

• Solución

El volumen de una caja rectangular es simplemente el producto de sus tres dimensiones:

V = 34 cm × 22 cm× 8 cm = 5984 cm³

Ejercicio 2

La base de una pirámide cuadrangular tiene un área de 16 cm² y su altura es de 6 cm. Calcular el volumen de dicha pirámide.

• Solución

Se emplea la fórmula dada más arriba para el volumen de una pirámide, conocida el área de su base:

 Y se sustituyen los valores numéricos:

V = (1/3)× 16 cm² × 6 cm = 32 cm³