Peso (física): cálculo, unidades, ejemplos, ejercicios
El peso es la fuerza con que la Tierra atrae a los objetos a su superficie. Cada vez que se deja caer un objeto, este va a parar al suelo, no es capaz de subir por sus propios medios ni se queda ingrávido a mitad de camino, lo cual se debe a que la Tierra lo atrae.
Todos los objetos invariablemente se atraen entre sí, incluso los más pequeños, solo que la magnitud de la fuerza con que lo hacen es proporcional a la masa. Esto significa que los objetos con masa pequeña ejercen poca fuerza sobre otros, pero los cuerpos celestes como la Tierra, sí son capaces de ejercer una fuerza muy grande.

La Tierra mantiene a la Luna orbitando a su alrededor gracias a esta fuerza de atracción, la cual se llama atracción gravitatoria cuando se trata de objetos que se encuentran lejos de la superficie terrestre, y peso cuando los objetos están cercanos.
De esto se deduce que la fuerza de gravedad no requiere que los objetos estén necesariamente en contacto unos con otros para poder actuar: por eso se dice que es una fuerza de acción a distancia.
Los objetos siguen teniendo peso aunque se encuentren a cierta altura sobre el suelo y cuanta más masivos sean, mayor será este peso.
El gran científico inglés Isaac Newton fue el primero en dar una explicación acerca de esta cuestión, a través la ley de gravitación universal que lleva su nombre y que desde entonces ha servido para entender cómo interaccionan los objetos con masa. Esto es muy importante, dado que cualquier objeto en el planeta tiene peso.
Índice del artículo
- 1 Unidades del peso
- 2 Cálculo del peso y fórmula
- 3 El peso como vector
- 4 Diferencias entre peso, masa y volumen
- 5 Ejemplos de peso
- 6 Ejercicio resuelto
- 7 Referencias
El Sistema Internacional de unidades SI tiene como unidad para el peso el newton, nombrado así en honor a Isaac Newton. Esta es la unidad para medir fuerzas de todo tipo.
El newton, abreviado N, se define como la fuerza necesaria para que un objeto de 1kg de masa adquiera una aceleración de 1m/s2. Aparte del newton, hay otras unidades de fuerza de uso común, por ejemplo las siguientes:
El kilogramo-fuerza o kilopondio, abreviado kg-f o kp, aunque comúnmente llamado kg sin más, es la fuerza que la Tierra ejerce sobre un objeto que está a la altura del nivel del mar y a 45º de latitud norte. Es preciso especificar la ubicación, ya que como se dijo, el campo gravitatorio experimenta variaciones con la altura y la latitud.
Cuando alguien dice que pesa 45 kg, en realidad lo que quiere decir es que su peso es de 45 kg-f, porque el kilogramo es la unidad reservada para la masa.
La equivalencia entre kg-f y N es: 1kg-f = 9.8 N
La libra-fuerza, abreviada lb-f es también una unidad de fuerza que es análoga a los kg-f, ya que es la fuerza que la Tierra ejerce sobre un objeto de 1 lb de masa. Y al igual que con los kg-f, no hay problema con los valores cuando se está en la Tierra, es decir, un objeto de l lb de masa, pesa 1 lb-f.
La equivalencia en lb-f y N es: 1 lb-f ≡ 4,448222 N.
El peso de un objeto es proporcional a su masa. A mayor masa, mayor peso.
La fórmula para hallar la magnitud del peso P (o también W, como algunas veces se lo denota, por “weight” en inglés) es muy sencilla:
P = mg
Donde m representa la masa del objeto y g es la magnitud de la aceleración de la gravedad (intensidad del campo gravitatorio o gravedad), aproximadamente constante y cuyo valor se toma como 9.81 m/s2 para los cálculos más frecuentes.
El peso es un vector y para distinguir entre un vector y su magnitud se utilizan las letras negritas. De esta forma, cuando se habla de P se entiende que es el valor numérico y cuando se escribe P se hace referencia al vector:
P = m∙g
La g con letra negrita es el campo gravitatorio terrestre, es decir, la influencia que ejerce la Tierra en el espacio que la rodea, independientemente de si hay o no otro cuerpo que la perciba. Cualquier objeto con masa tiene un campo gravitatorio propio, ya sea pequeño o grande.
La intensidad del campo gravitatorio terrestre g no es del todo constante. Tiene pequeñas variaciones que surgen principalmente debido a que la Tierra no es una esfera perfecta y también a las diferencias de altura y densidad locales. Pero para la mayoría de las aplicaciones, el valor 9.81 m/s2 funciona muy bien.
Otros cuerpos celestes tienen su propio campo gravitatorio característico, por lo tanto la aceleración de la gravedad difiere según el planeta o satélite. Un mismo objeto tendría un peso distinto en cada uno, de allí que el peso no es una propiedad característica de las cosas, pero sí de la materia en general.
El peso es un vector y por tanto tiene magnitud, dirección y sentido. En las cercanías de la superficie terrestre, el peso es un vector en dirección vertical y el sentido es siempre hacia abajo.
Por lo general, la dirección vertical se nombra como eje y o z, y al sentido hacia abajo se le asigna signo + o signo – para distinguirlo del sentido hacia arriba. La elección depende de la ubicación del origen. En la imagen inferior, el origen se escogió en el punto desde el cual cae la manzana:

El vector unitario j, un vector de magnitud igual 1, se utiliza para señalar y distinguir la dirección vertical. En términos de este vector, el peso se escribe así:
P = mg (− j)
Donde se asigna signo negativo al sentido hacia abajo.

Con frecuencia estos tres conceptos se confunden, pero revisando las características del peso, es fácil diferenciarlo de la masa y del volumen.
Para empezar, el peso depende del campo gravitatorio del lugar donde esté el objeto. Por ejemplo, en la Tierra y en la Luna una misma cosa tiene un peso diferente, aunque la cantidad de átomos que la compongan se mantenga constante.
La masa es una magnitud escalar, relacionada con la cantidad de átomos que componen al objeto y se pone en evidencia con la resistencia que el objeto tiene a cambiar su movimiento, una propiedad llamada inercia.
Por su parte, el volumen es la medida del espacio que ocupa un objeto, otra cantidad escalar. Dos objetos con igual volumen no pesan lo mismo, por ejemplo un cubo de hierro pesa mucho más que otro de poliestireno de las mismas dimensiones.
En resumen:
- La masa está relacionada con la cantidad de materia que posee un cuerpo.
- El peso es la fuerza que ejerce la Tierra sobre dicha masa, proporcional a ella.
- El volumen es el espacio ocupado por la materia.
Hay que destacar que siendo cantidades escalares, ni la masa ni el volumen tienen dirección o sentido, sino solamente valor numérico y una unidad adecuada. En cambio el peso, al ser un vector, siempre debe expresarse correctamente señalando la magnitud, la unidad, la dirección y el sentido, como en la sección previa.
Todos los objetos en la Tierra tienen peso, hasta se pueden “pesar” objetos que no están en la Tierra, como otros planetas o el Sol, aunque por medios indirectos, claro está.
Como el rango de pesos es muy grande, se utiliza la notación científica (en potencias de 10) para expresar algunos que son muy grandes o muy pequeños:
-El Sol: 1,989 × 1030 kg-f
–Júpiter: 1,898 × 1027 kg-f
-Un mosquito: 2.0 × 10-5 N
-Bebés: 34.3 N
-Un niño: 353 N
-Persona adulta: 65 kg-f
-Un elefante adulto: 5.5 × 103 kg-f
-Ballena azul: 1.0 × 106 N
Una caja de masa 20 kg reposa sobre una mesa.
a) Hallar el peso de la caja y la fuerza normal que la mesa ejerce sobre ella.
b) Se coloca otra caja de 10 kg sobre la primera. Encontrar la normal que ejerce la mesa sobre la caja de 20 kg y la normal que esta ejerce sobre la caja más pequeña.
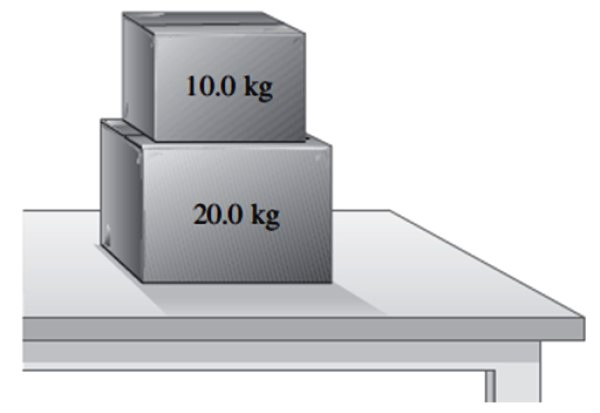
Solución a
Es conveniente hacer un diagrama de cuerpo libre sobre la caja, el cual consiste en dibujar las fuerzas que actúan sobre ella.
En esta situación, aún no está la caja más pequeña encima, por lo tanto hay solamente dos fuerzas: la primera es el peso P que se dibuja verticalmente hacia abajo, conforme se indicó en las secciones precedentes y luego está la normal N, que es la fuerza perpendicular que ejerce la mesa e impide que la caja caiga.
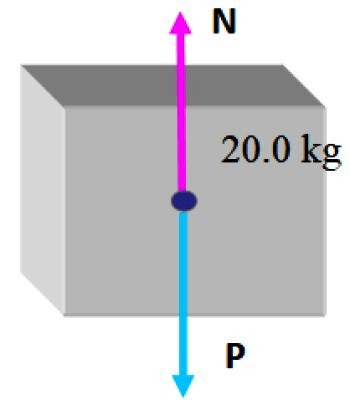
Dado que la caja se encuentra en equilibrio estático en estas circunstancias, es razonable concluir que la magnitud de la normal es la misma que la del peso, para que lo pueda compensar, por lo tanto:
N = mg = 20.0 kg x 9.8 m/s2 = 196 N; dirigida verticalmente hacia arriba.
Por su parte el peso es P = 196 N dirigido verticalmente hacia abajo.
Solución b
Ahora se hacen nuevos diagramas de cuerpo libre sobre ambos objetos. Para la caja grande las cosas cambian un poco, ya que la caja pequeña ejerce fuerza sobre ella.
Las fuerzas son como sigue: N y P son respectivamente la normal que ejerce la mesa y el peso sobre la caja de 20.0 kg, eso no cambió. Y la nueva fuerza ejercida por la caja pequeña es N1, la normal debida al contacto con la cara superior de la caja grande.
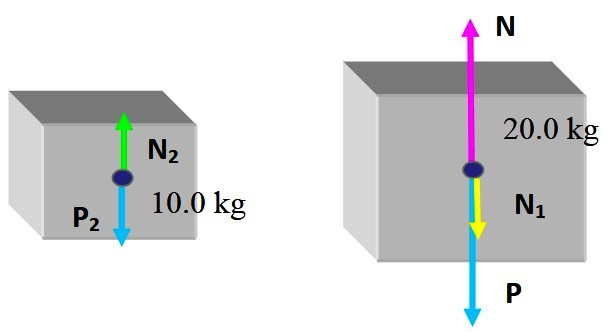
En cuanto a la caja pequeña, esta recibe la normal N2, ejercida por la cara superior de la caja grande y por supuesto su peso P2. Dado que las cajas están equilibrio estático:
N2 – P2 = 0
N – N1 – P = 0
De la primera ecuación se tiene que N2 = P2 = 10 kg x 9.8 m/s2 = 98 N. Por ley de acción y reacción, la magnitud de la fuerza que la caja pequeña recibe, es la misma que esta ejerce sobre la caja grande, entonces:
N2 = N1 = 98 N
De la segunda ecuación se despeja la normal N que ejerce la mesa sobre la caja grande, que a su vez tiene la caja pequeña encima:
N = N1 + P = 98 N + 196 N = 294 N
- Figueroa, D. 2005. Serie: Física para Ciencias e Ingeniería. Volumen 2. Dinámica. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Physics. 2nd. Ed. McGraw Hill.
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1. Pearson.
- Serway, R., Jewett, J. 2008. Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
- Thomas Griffith, W. 2007. Física Conceptual. Mc Graw Hill.
