Ángulo

Otra forma de definir al ángulo es como la región que se forma a partir de la unión de la intersección o unión de dos rectas que comparten un vértice o punto en común.

Los ángulos entonces pueden formarse a partir de rectas o semirrectas que se intersecan. En este punto, es importante recordar que la recta es un elemento unidimensional que se constituye por una sucesión de puntos que se extiende de forma indefinida, es decir, no tiene inicio ni final. Asimismo, la semirrecta es la porción de la recta que parte de un punto de la misma y se prolonga al infinito, es decir, tiene un origen, pero no un final.

Entonces, los ángulos se pueden formar en un plano cuando trazamos rectas o semirrectas, como observamos abajo.

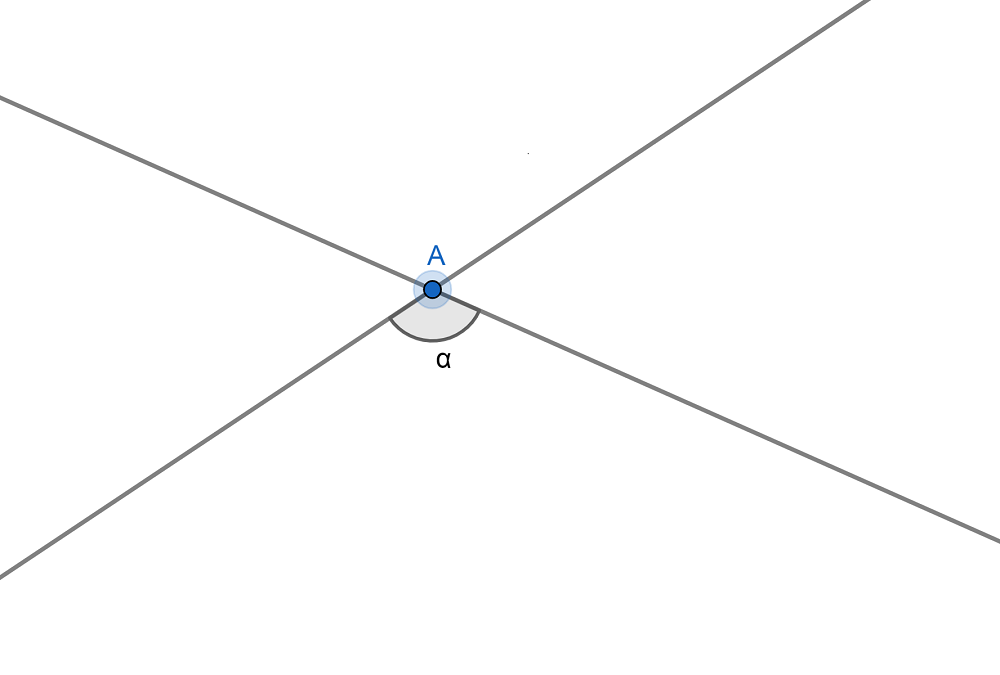
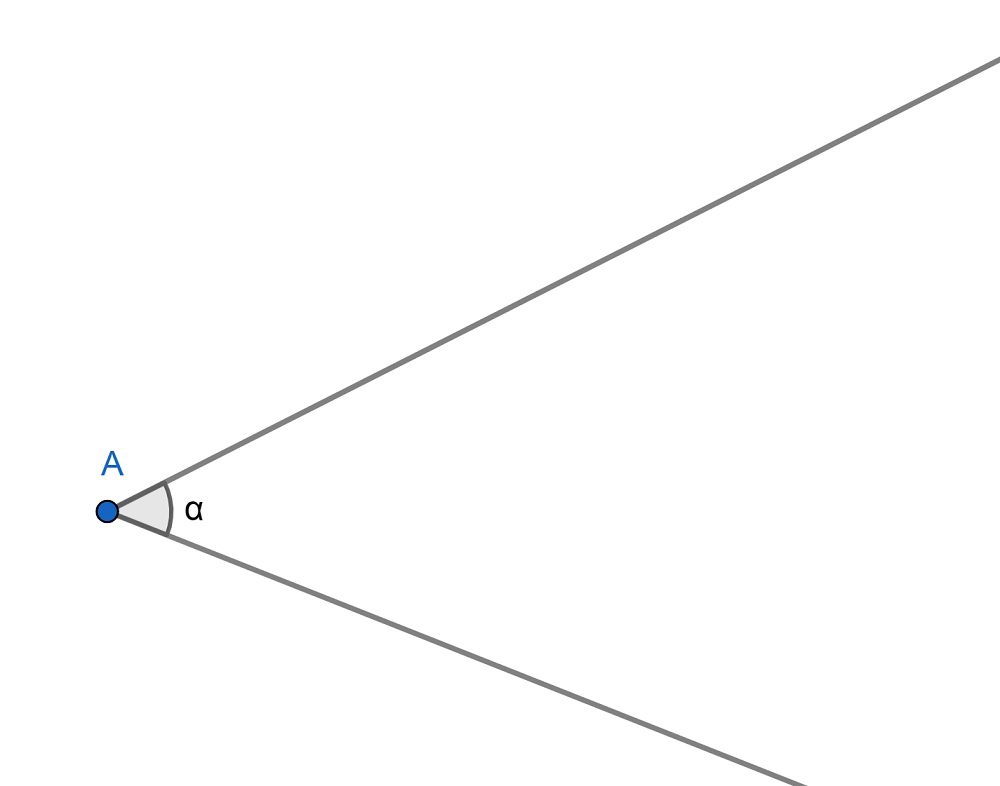
Por otro lado, también se forman ángulos por la unión de segmentos que comparten un vértice. Debemos recordar que un segmento es una porción de recta que está acotada por dos puntos, tiene un origen y un final.

Los ángulos que se forman a partir de segmentos los podemos observar en los polígonos, como en la figura de abajo donde α, β y γ son los ángulos internos del triángulo.

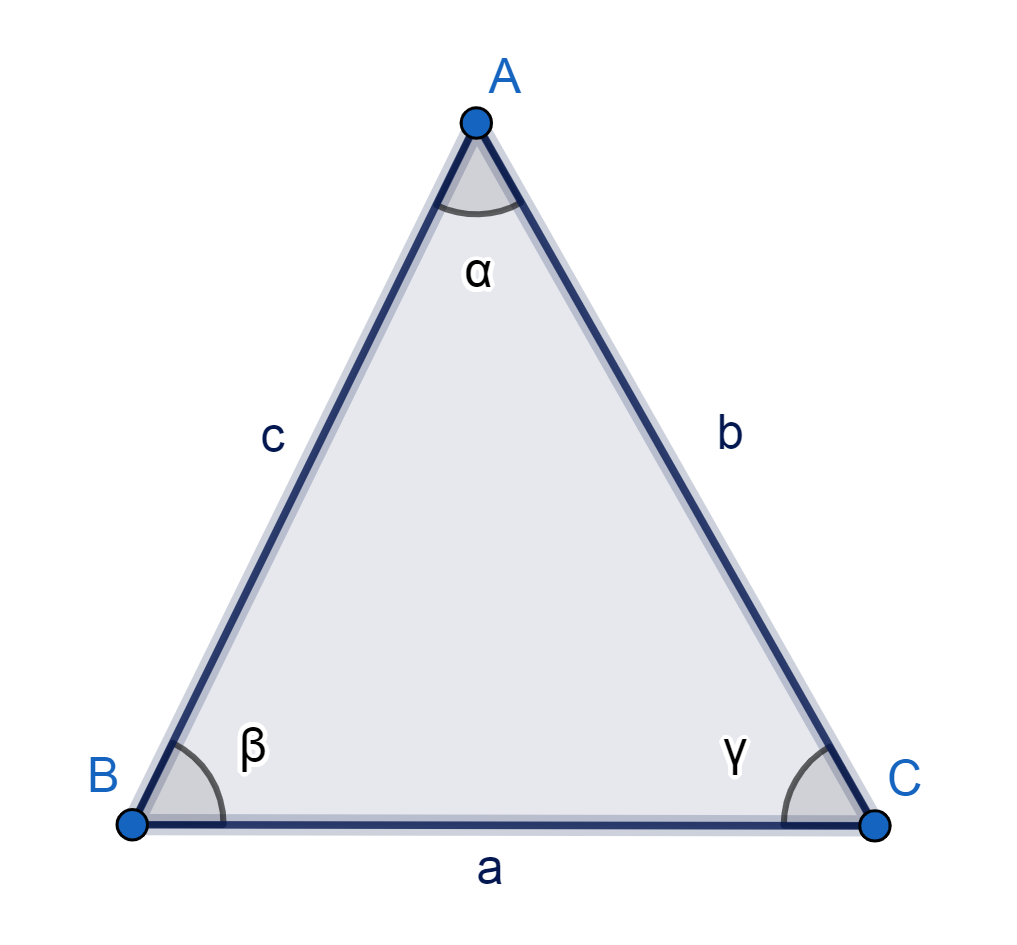
Cabe aclarar además que un ángulo puede formarse entre dos vectores que son segmentos segmentos de rectas que siguen una determinada dirección.

Según su medida, los ángulos se pueden ser:

• Agudo: Mide menos de 90º o π/2 radianes.

• Obtuso: Mide más de 90º o π/2 radianes y menos de 180º o π radianes.

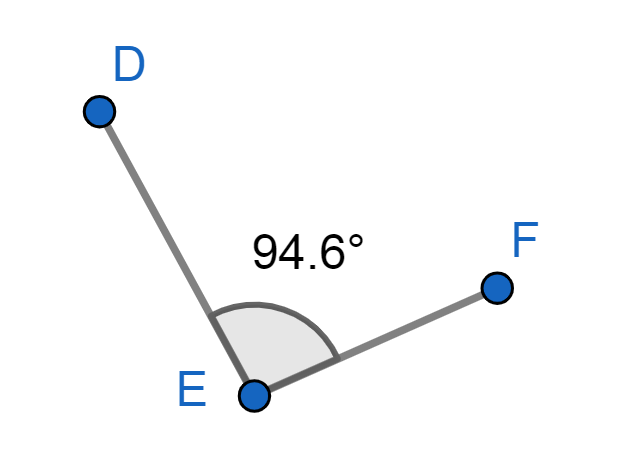
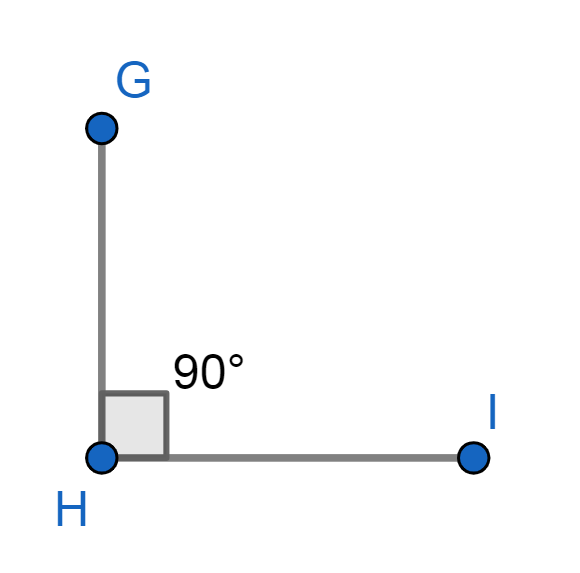
• Recto: Es igual a 90º o π/2 radianes.

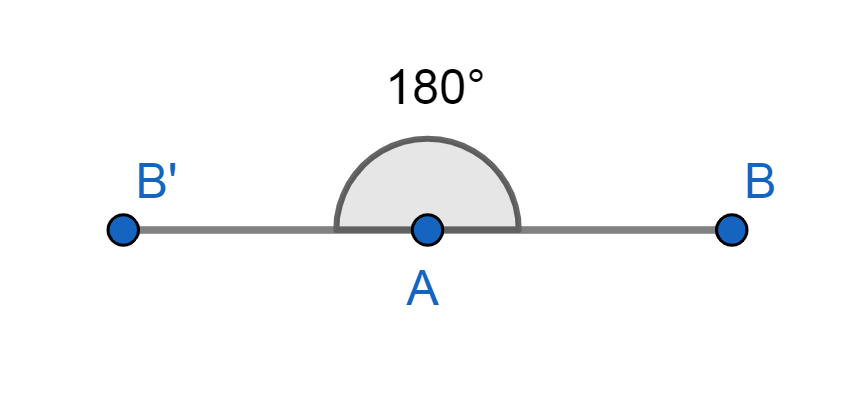
• Llano: Su medida es de 180º o π radianes.

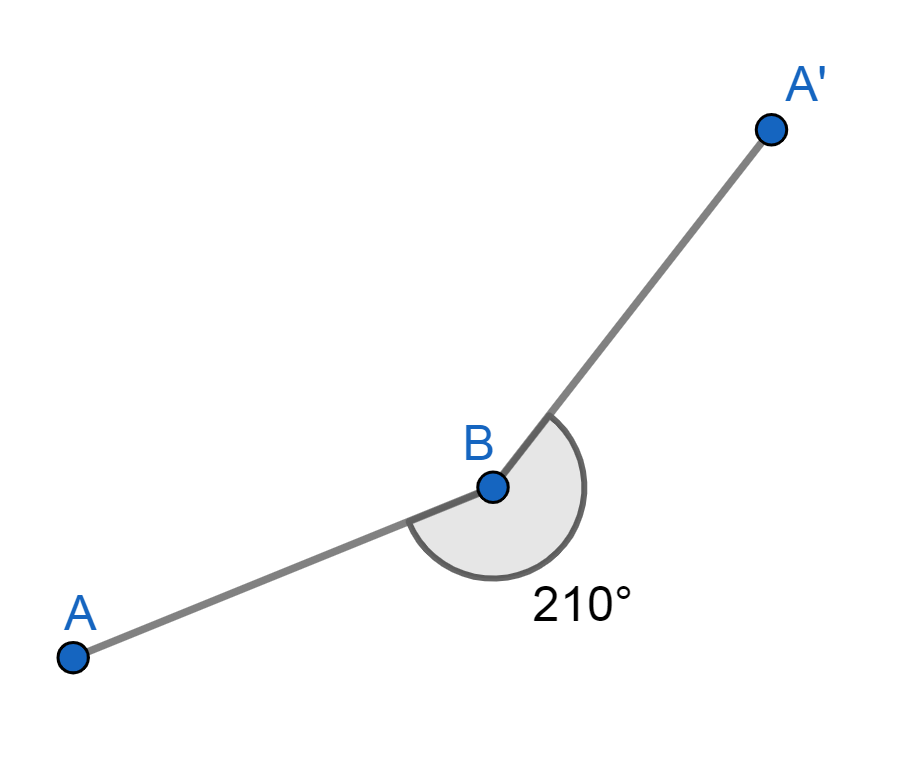
• Oblicuo o cóncavo: Mide más de 180º o π radianes y menos de 360º o 2π radianes (cabe señalar que un ángulo convexo es aquel que mide menos de 180º).

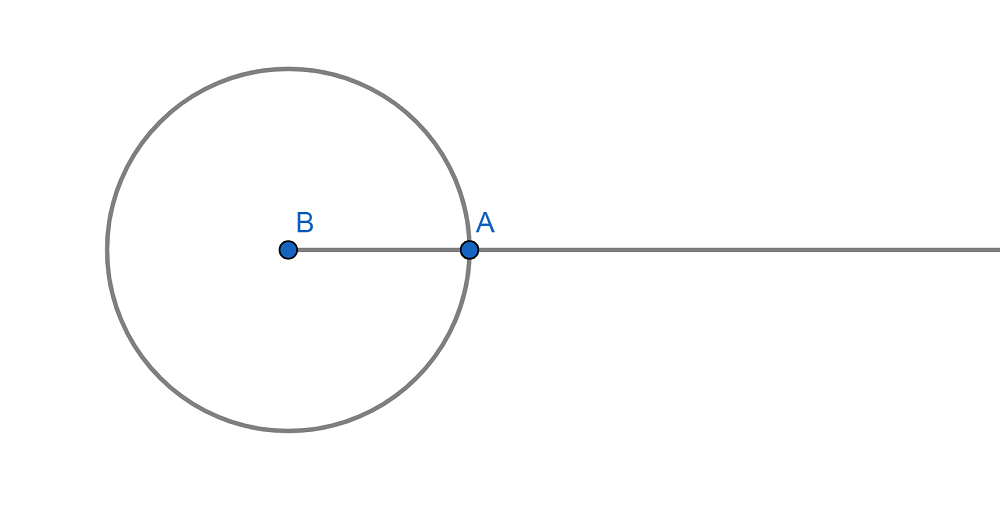
• Completo o perigonal: Mide exactamente 360º o 2π radianes

De acuerdo a cómo se ubican uno respecto a otro, los ángulos pueden ser:

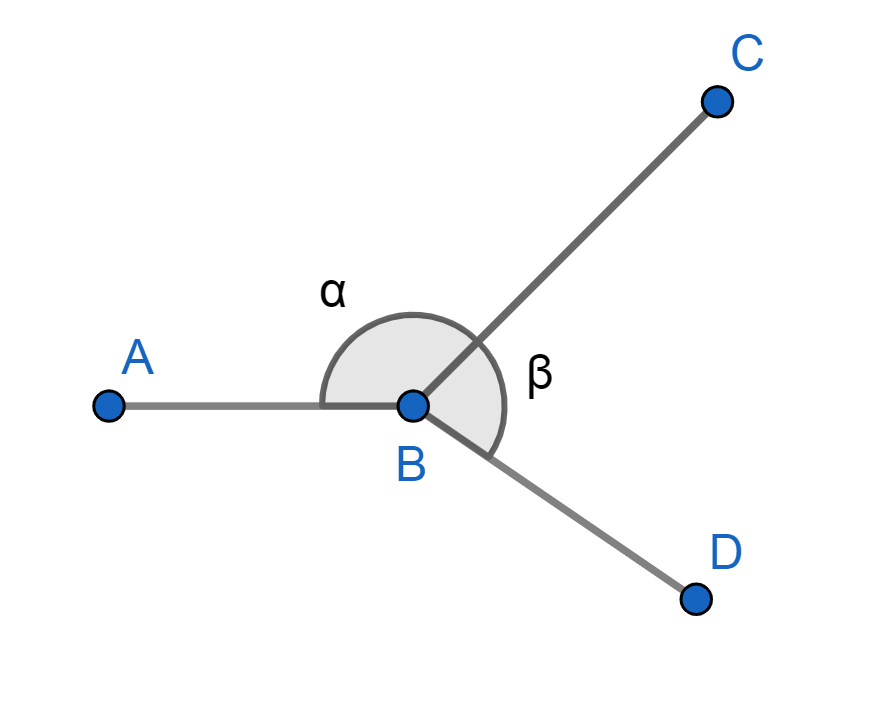
• Consecutivos: Se encuentran uno contiguo al otro. En la imagen de abajo, α y β son ángulos consecutivos.

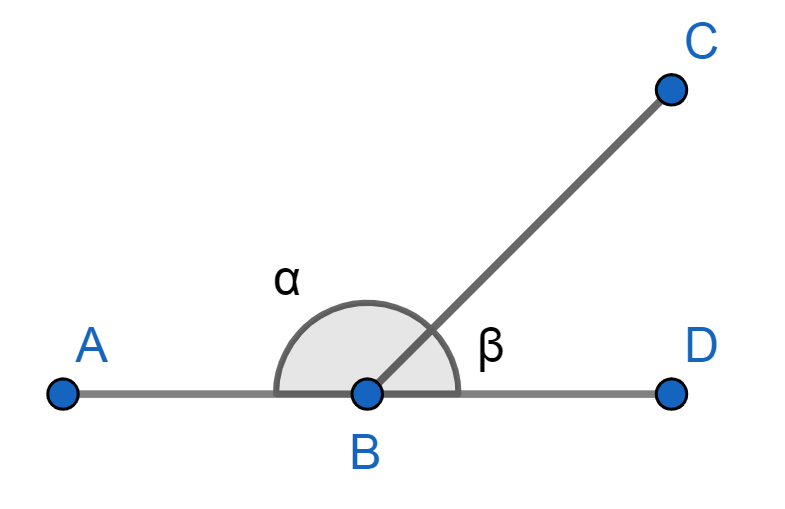
• Adyacentes: Forman parte de la misma recta y suman un ángulo llano, es decir, suman 180º, como α y β en el siguiente gráfico:

• Opuestos por el vértice: Comparten el mismo vértice y uno se constituye por la extensión de los lados que forman el otro ángulo. En la imagen de abajo, α y δ son opuestos por el vértice, al igual que β y γ.

Finalmente, de acuerdo con el resultado de su sumatoria, los ángulos pueden ser:

• Complementarios: Suman 90º.
• Suplementarios: Su sumatoria es de 180º.

En la imagen de abajo, α y β son complementarios. En tanto, δ y ε son suplementarios.

Para la medición de un ángulo puede recurrir principalmente a dos métodos:

• Sistema sexagesimal: Es aquel que, tomando como referencia el ángulo que se observa en una superficie plana (al que llamamos ángulo llano, como ya explicamos), se divide en 180 partes iguales llamadas grados. Asimismo, cada grado subdivide en 60 minutos, y cada minuto en 60 segundos.
• Sistema de radianes: El ángulo completo o perigonal, que representa una circunferencia, se puede calcular dividiendo la longitud del arco (que es igual a 2πr como explicamos en el artículo de circunferencia) entre el radio de la figura:

α=L/r=2πr/r=2r

A partir de ese dato, deducimos que el ángulo llano es π, por ejemplo, y que el ángulo recto es π/2.