Modelo de Romer
El Modelo de Romer establece que cuando se dan externalidades tecnológicas positivas se debe a la acumulación del factor K. En este caso, K no se refiere exclusivamente al capital físico, sino que incorpora el conocimiento dentro de la variable.
Paul Romer creó, en el año 1986, un modelo donde se introdujeron externalidades del capital. En dicho modelo, se considera que cuando una empresa incrementa su stock de capital mediante la inversión, no aumenta únicamente su producción. En este caso, también se produciría un incremento en la producción del resto de empresas del sector.
El motivo por el que sucede esto, es que cuando se realiza un proceso de investigación, se adquieren tanto conocimientos como experiencias que son utilizadas por las compañías que llevan a cabo una actividad económica igual o parecida.
Supuestos del modelo de Romer
Para poder comprender correctamente las causas del crecimiento en el modelo de Romer, es necesario distinguir entre las ideas y los objetos. A continuación te mostramos los cuatro supuestos del modelo:
- Producción de objetos:
- Para producirlos son necesarios tanto conocimientos como trabajo. Los objetos aislados tienen rendimientos constantes de escala, sin embargo, los objetos junto a las ideas, poseen rendimientos crecientes a escala.
- En la siguiente ecuación At hace referencia a las ideas y Lyt es el trabajo.
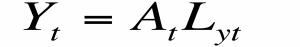
- Producción de ideas:
- La producción de ideas depende de: las ideas existentes en el período anterior, el número de trabajadores que las producen y de su productividad.
- En esta caso Z hace referencia a la productividad.
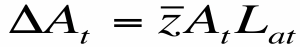
- Restricción de recursos:
- La suma del número de trabajadores que producen ideas y el número de trabajadores que producen objetos es igual a la población ocupada.
- La población ocupada es N.
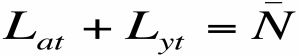
- Asignación de trabajo:
- En el modelo original, Romer considera mercados de trabajo y de productos. A su vez, introduce patentes y el poder de monopolio para tener en cuna la cuestión de los rendimientos crecientes. Para simplificar dicho modelo, supondremos que una proporción de la población es la que produce ideas.
- Por último, «l» es la proporción de población que produce ideas.
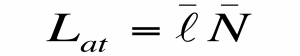
Resolución del modelo de Romer
Como hemos visto en el apartado anterior, el modelo se compone de cuatro ecuaciones. Cada ecuación consta de cuatro incógnitas y, junto a esto, también se plantean cuatro parámetros:
- Incógnitas:
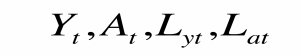
- Parámetros:
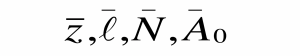
Para resolver dicho modelo, es necesario calcular el valor de equilibrio de las variables endógenas en función de los parámetros:
- Fórmula 1:
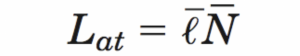
- Fórmula 2:
- Fórmula 3:
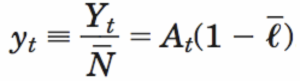
La producción por persona es proporcional a At y depende del acervo total de conocimientos:
- Una nueva idea que eleve At hace incrementar la producción de cada persona que hay en la economía. Por ejemplo, en el caso del modelo de Solow, la producción por persona depende del capital por persona y no del stock de K agregado.
- Para calcular el acervo de conocimientos At, es necesario el siguiente planteamiento:
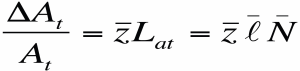
- Donde:
- La tasa de crecimiento de los conocimientos es constante.
- Para simplificar la notación:
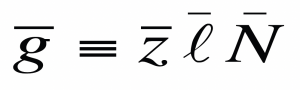
- Por tanto, At viene dado por:
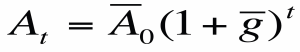
- Sustituyendo en la función de producción per cápita, obtenemos:
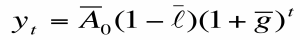
- El PIB per cápita crece a una tasa constante que viene dada por la función de los parámetros del modelo:
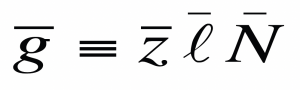
- Representación gráfica:

Conclusiones
En el modelo de Romer, las ideas y el trabajo, de forma conjunta, poseen rendimientos crecientes, ya que los rendimientos de las ideas no tienen límites. En este modelo, existe una senda de crecimiento equilibrado en la que las tasas de crecimiento de todas las variables son constantes e iguales a:
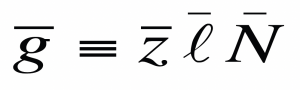
En comparación con el modelo de Solow, en este modelo no existe una dinámica de transición en la que la tasa de crecimiento va disminuyendo conforme más se aproxima la economía al estado estacionario.
Por último, si se produce un incremento en la población o en el número de productores de ideas, se eleva de forma inmediata la tasa de crecimiento de la producción per cápita.
