Matriz regular
Una matriz regular de orden n es una matriz que tiene el mismo número de filas y de columnas y su determinante es distinto de cero (0).
En otras palabras, una matriz regular de orden n es una matriz cuadrada a partir de la cual podemos obtener la matriz inversa.
Fórmula matriz regular
Dada una matriz V con el mismo número de filas (n) y columnas (m), es decir, m=n, y con determinante distinto de cero (0), entonces decimos que V es una matriz regular de orden n.
Aplicación
La matriz regular se utiliza como etiqueta para las matrices que cumplen las condiciones para tener matriz inversa.
- La matriz es una matriz cuadrada.
El número de filas (n) tiene que ser el mismo que el número de columnas (m). Es decir, el orden de la matriz tiene que ser n dado que n=m.
- La matriz tiene determinante y este es distinto de cero (0).
El determinante de la matriz debe ser distinto de cero (0) porque se utiliza como denominador en la fórmula de la matriz inversa.
Ejemplo teórico
¿Es la matriz D una matriz cuadrada e invertible?
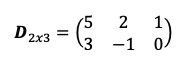
- Comprobamos si la matriz D cumple con los requisitos para ser una matriz regular.
- ¿Es la matriz D una matriz cuadrada?
El número de columnas de la matriz D es distinto al número de filas dado que hay 2 filas y 3 columnas. Por tanto, la matriz D no es una matriz cuadrada ni tampoco una matriz regular.
La primera condición para ser una matriz regular (condición de matriz cuadrada) es un requisito necesario y suficiente ya que si no se cumple implica directamente que la matriz no es una matriz regular y por tanto no podremos calcular su determinante.
- ¿Es la matriz D invertible?
Dado que la matriz D no es cuadrada, no podemos calcular su determinante y decidir si este es distinto o igual a cero (0).
Ejemplo práctico
Matriz regular de orden 2
¿Es la matriz U una matriz cuadrada e invertible?
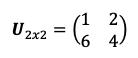
- Comprobamos si la matriz U cumple con los requisitos para ser una matriz regular.
- ¿Es la matriz U una matriz cuadrada?
El número de filas y el número de columnas coincide en la matriz U. Entonces, la matriz U es una matriz cuadrada de orden 2.
- ¿Es la matriz U invertible?
Primero tendremos que calcular el determinante de la matriz y después comprobar que es distinto de cero (0).
- Determinante de la matriz U:
- Comprobar que la matriz U es invertible:
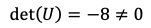
Entonces, la matriz U es una matriz regular dado que es una matriz cuadrada e invertible.
