Distribución normal
La distribución normal es un modelo teórico capaz de aproximar satisfactoriamente el valor de una variable aleatoria a una situación ideal.
En otras palabras, la distribución normal adapta una variable aleatoria a una función que depende de la media y la desviación típica. Es decir, la función y la variable aleatoria tendrán la misma representación pero con ligeras diferencias.
Una variable aleatoria continua puede tomar cualquier número real. Por ejemplo, las rentabilidades de las acciones, los resultados de un examen, el coeficiente de inteligencia IQ y los errores estándar son variables aleatorias continuas.
Una variable aleatoria discreta toma valores naturales. Por ejemplo, el número de estudiantes en una universidad.
La distribución normal es la base de otras distribuciones como la distribución t de Student, distribución ji-cuadrada, distribución F de Fisher y otras distribuciones.
Fórmula de la distribución normal
Dada una variable aleatoria X, decimos que la frecuencia de sus observaciones puede aproximarse satisfactoriamente a una distribución normal tal que:
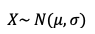
Donde los parámetros de la distribución son la media o valor central y la desviación típica:

En otras palabras, estamos diciendo que la frecuencia de una variable aleatoria X puede representarse mediante una distribución normal.
Representación
Función de densidad de probabilidad de una variable aleatoria que sigue una distribución normal.
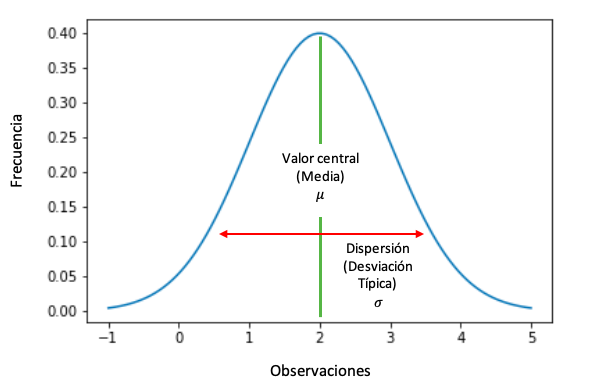
Propiedades
- Es una distribución simétrica. El valor de la media, la mediana y la moda coinciden. Matemáticamente,
Media = Mediana = Moda
- Distribución unimodal. Los valores que son más frecuentes o que tienen más probabilidad de aparecer están alrededor de la media. En otras palabras, cuando nos alejamos de la media, la probabilidad de aparición de los valores y su frecuencia descienden.
¿Qué necesitamos para representar una distribución normal?
- Una variable aleatoria.
- Calcular la media.
- Calcular la desviación típica.
- Decidir la función que queremos representar: función de densidad de probabilidad o función de distribución.
Ejemplo teórico
Suponemos que queremos saber si los resultados de un examen pueden aproximarse satisfactoriamente a una distribución normal.
Sabemos que en este examen participan 476 estudiantes y que los resultados podrán oscilar entre 0 y 10. Calculamos la media y la desviación típica a partir de las observaciones (resultados del examen).
Entonces, definimos la variable aleatoria X como los resultados del examen que depende de cada resultado individual. Matemáticamente,
El resultado de cada estudiante se anota en una tabla. De esta forma, obtendremos una visión global de los resultados y de su frecuencia.
| Resultados | Frecuencia |
| 0 | 20 |
| 1 | 31 |
| 2 | 44 |
| 3 | 56 |
| 4 | 64 |
| 5 | 66 |
| 6 | 62 |
| 7 | 51 |
| 8 | 39 |
| 9 | 26 |
| 10 | 16 |
| TOTAL | 475 |
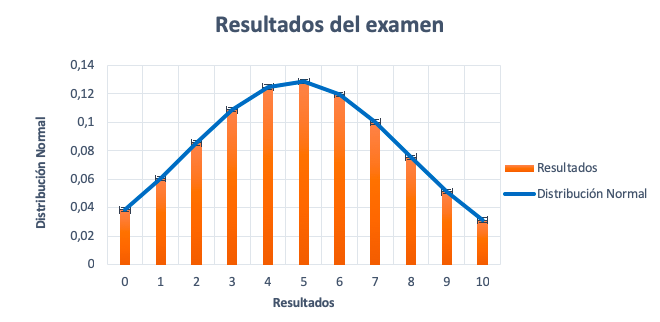
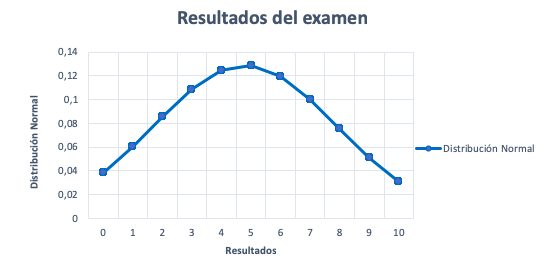
Una vez hecha la tabla, representamos los resultados del examen y las frecuencias. Si el gráfico se parece a la imagen anterior y cumple con las propiedades, entonces, la variable resultados del examen puede aproximarse satisfactoriamente a una distribución normal de media 4,86 y desviación típica de 2,56.
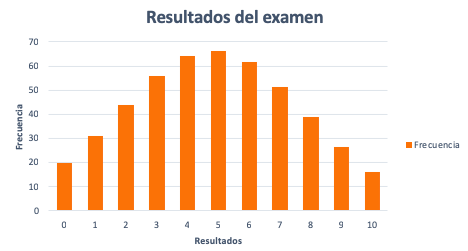
¿Los resultados del examen pueden aproximarse a una distribución normal?
Razones para considerar que la variable resultados del examen sigue una distribución normal:
- Distribución simétrica. Es decir, existe el mismo número de observaciones tanto a la derecha como a la izquierda del valor central. También, que la media, la mediana y la moda tienen el mismo valor.
Media = Mediana = Moda = 5
- Las observaciones con más frecuencia o probabilidad están alrededor del valor central. En otras palabras, las observaciones con menos frecuencia o probabilidad se encuentran lejos del valor central.
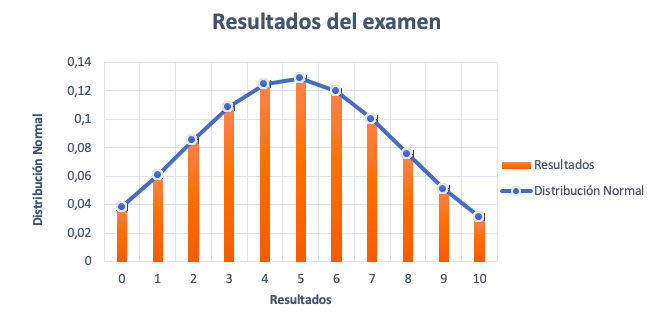
La distribución normal describe la variable aleatoria mediante una aproximación que produce errores estándar (las barras encima de cada columna). Estos errores son la diferencia entre las observaciones reales (resultados) y la función de densidad (distribución normal).