Distribución t de Student
La distribución t de Student o distribución t es un modelo teórico utilizado para aproximar el momento de primer orden de una población normalmente distribuida cuando el tamaño de la muestra es pequeño y se desconoce la desviación típica.
En otras palabras, la distribución t es una distribución de probabilidad que estima el valor de la media de una muestra pequeña extraída de una población que sigue una distribución normal y de la cual no conocemos su desviación típica.
Artículos recomendados: grados de libertad, grados de libertad (ejemplo) y distribución normal.
Fórmula de la distribución t de Student
Dada una variable aleatoria continua L, decimos que la frecuencia de sus observaciones puede aproximarse satisfactoriamente a una distribución t con g grados de libertad tal que:
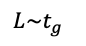
Representación de la distribución t de Student
Función de densidad de una distribución t con 3 grados de libertad (df).
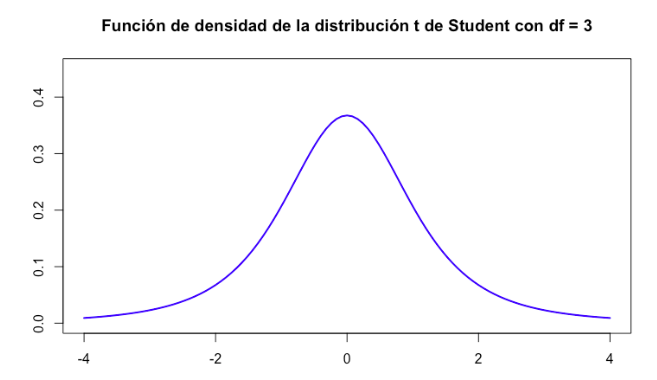
Como podemos ver, la representación de la distribución t se parece mucho a la distribución normal salvo que la distribución normal tiene las colas más anchas y es más apuntalada. En otras palabras, deberíamos añadir más grados de libertad a la distribución t para que la distribución “crezca” y se parezca más a la distribución normal.
Especialidad
Y… ¿Por qué es tan especial la distribución t?
Pues porqué a diferencia de la distribución normal que depende de la media y la varianza, la distribución t solo depende de los grados de libertad, del inglés, degrees of freedom (df). En otras palabras, controlando los grados de libertad, controlamos la distribución.
Aplicación de la t de Student
La distribución t se utiliza cuando:
- Queremos estimar la media de una población normalmente distribuida a partir de una muestra pequeña.
- Tamaño de la muestra es inferior a 30 elementos, es decir, n < 30.
A partir de 30 observaciones, la distribución t se parece mucho a la distribución normal y, por tanto, utilizaremos la distribución normal.
- No se conoce la desviación típica o estándar de una población y tiene que ser estimada a partir de las observaciones de la muestra.
Ejemplo
Suponemos que tenemos 28 observaciones de una variable aleatoria G que sigue una distribución t de Student con 27 grados de libertad (df).

Matemáticamente,
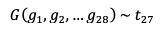
Dado que estamos trabajando con datos reales, siempre habrá un error de aproximación entre los datos y la distribución. En otras palabras, la media, mediana y moda no siempre serán cero (0) o exactamente iguales.
Representamos la frecuencia de cada observación de la variable G mediante un histograma.
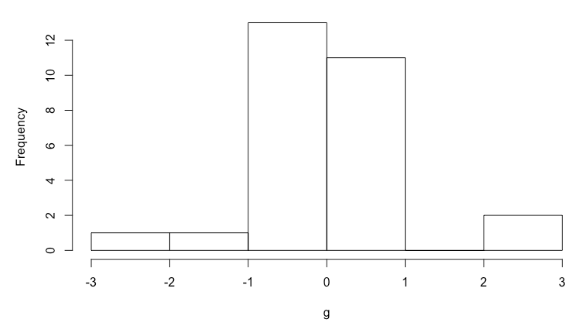
¿La variable aleatoria G puede aproximarse a una distribución t?
Razones para considerar que la variable G sigue una distribución t:
- La distribución es simétrica. Es decir, existe el mismo número de observaciones tanto a la derecha como a la izquierda del valor central. También, que la media y la mediana tienden a aproximarse al mismo valor. La media es aproximadamente cero, media = 0,016.
- Las observaciones con más frecuencia o probabilidad están alrededor del valor central. Las observaciones con menos frecuencia o probabilidad se encuentran lejos del valor central.
