Función matemática

En otras palabras, la variable dependiente (Y) toma valores determinados en función (dependiendo) de los valores que tome la variable independiente (X). 

Definimos: 

Variable independiente = X={x_1, x₂,…, x_n}.

Variable dependiente = Y={y₁, y₂ ,…, y_n}.

La expresión “estar en función de” se puede entender como “ser dependiente de”. Es decir, la variable Y es función de la variable X. La variable Y se denomina variable dependiente precisamente por el motivo de depender de los valores que tome la variable independiente X. De la misma forma, se denomina variable independiente porque su valor no depende de ninguna variable expresada en la función. 

Generalmente, para cada valor de la variable independiente X solo le corresponde un único valor de la variable dependiente Y.  Esta afirmación es cierta siempre y cuando no tengamos en cuenta otros tipos de funciones que permitan a la variable dependiente Y tener más de un valor de la variable independiente X asociado. Es decir, existen funciones donde una variable dependiente Y, puede estar relacionada con más de un valor de la variable independiente X.  Este tipo de funciones se llaman funciones suryectivas. 

Las funciones utilizan ecuaciones para representar la relación de dependencia entre la variable dependiente y la independiente. Entonces, la expresión matemática de las equaciones son las funciones. Gracias a las funciones, podemos representar las equaciones en los gráficos. 

En microeconomía utilizamos las funciones cuando queremos expresar la utilidad de los agentes que participan en la economía. En finanzas, cuando queremos expresar el perfil de riesgo de un agente expuesto a una situación de incertidumbre. En econometría, las regresiones tanto lineales como no lineales también son funciones.

Las funciones principalmente pueden clasificarse según su naturaleza y condición:

1. Funciones algebraicas. 
2. Funciones polinómicas.
3. Funciones a trozos. 
4. Funciones racionales. 
5. Funciones radicales. 
6. Funciones trascendentes. 
7. Funciones inyectivas. 
8. Funciones suryectivas. 
9. Funciones byectivas.
10. Funciones no inyectivas y no suryectivas.

• Y=3X. 
  • La variable dependiente Y será los valores que tome la variable X multiplicados por 3. La pendiente de la recta es 3 y debe pasar por el origen de coordenadas. La representación gráfica es una recta. 

Gráfico de una función matemática lineal:

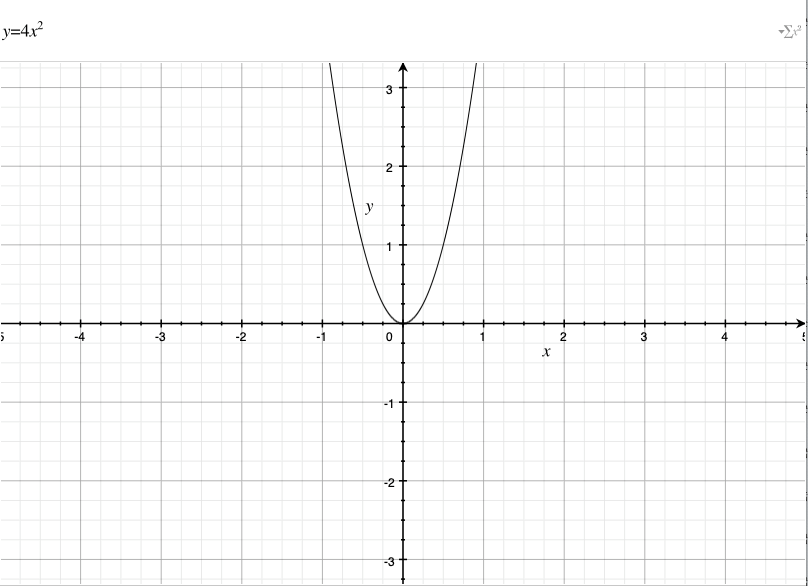
• Y=4X²
  • La variable dependiente Y será los valores que tome la variable X elevados al cuadrado y multiplicados por 4. La representación gráfica es una parábola.

Gráfico de una función matemática cuadrática: