Cuota de un crédito
La cuota de un crédito es el pago periódico que se compromete a realizar un deudor a su acreedor con el fin de devolver el financiamiento que éste le otorgó.
En la cuota se pueden distinguir dos componentes. El primero corresponde al reintegro de parte del capital prestado (llamado principal) mientras que el otro concierne a los intereses acumulados. Estos últimos se calculan multiplicando el tipo de interés del período por el saldo pendiente por cancelar.
Para explicarlo mejor podemos mostrar el siguiente ejemplo. Supongamos que se ha obtenido un crédito de US$ 15.000 a una tasa de interés de 3% mensual y con seis pagos a cancelar cada treinta días. Siguiendo el método de amortización francés, donde todas las cuotas son iguales, utilizamos la siguiente fórmula:

Entonces, el cuadro de amortización sería el siguiente:
| Intereses | Cuota | Principal | Saldo | |
|---|---|---|---|---|
| 15.000,00 | ||||
| 1 | 450,00 | 2.318,96 | 2.768,96 | 12.681,04 |
| 2 | 380,43 | 2.388,53 | 2.768,96 | 10.292,51 |
| 3 | 308,78 | 2.460,19 | 2.768,96 | 7.832,32 |
| 4 | 234,97 | 2.533,99 | 2.768,96 | 5.298,33 |
| 5 | 158,95 | 2.610,01 | 2.768,96 | 2.688,31 |
| 6 | 80,65 | 2.688,31 | 2.768,96 | – |
| suma | 1.613,78 | 15.000,00 | 16.613,78 |
Cálculo de la cuota
Para el cálculo de la cuota de un crédito debemos considerar en primer lugar el tipo de interés. Cuanto más alta sea la tasa, se elevarán más los gastos financieros y los pagos mensuales deberán ser mayores.
Igualmente, a mayor plazo de endeudamiento menor será la cuota mensual. Ello, tomando en cuenta que la devolución del principal se distribuirá entre un mayor número de pagos.
La cuota de un crédito depende además de otras variables como la cuota inicial y el plazo de gracia, en caso existieran en el contrato.
Cuota según método de amortización
La cuota varía en función a otro factor fundamental, el método de amortización financiera utilizado. Si es el francés, se calcularán la mensualidades de tal manera que todas sean iguales (Como en el ejemplo mostrado líneas arriba).
En el caso del método alemán, la cuota será variable. Con este sistema, la devolución del principal se divide en partes exactamente iguales, pero los intereses por pagar cambian, haciéndose cada vez más pequeños en la medida que quede menos del préstamo por cancelar.
Así, tendríamos como referencia la siguiente fórmula:
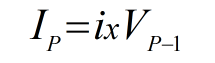

Si seguimos con el ejemplo planteado anteriormente, al usar el método alemán tendríamos el siguiente cuadro de amortización:
| Intereses | Cuota | Principal | Saldo | |
|---|---|---|---|---|
| 0 | 15.000,00 | |||
| 1 | 450,00 | 2.500,00 | 2.950,00 | 12.500,00 |
| 2 | 375,00 | 2.500,00 | 2.875,00 | 10.000,00 |
| 3 | 300,00 | 2.500,00 | 2.800,00 | 7.500,00 |
| 4 | 225,00 | 2.500,00 | 2.725,00 | 5.000,00 |
| 5 | 150,00 | 2.500,00 | 2.650,00 | 2.500,00 |
| 6 | 75,00 | 2.500,00 | 2.575,00 | – |
| suma | 1.575,00 | 15.000,00 | 1.6575,00 |
Finalmente, si se trata del método inglés todas las cuotas serán iguales, a excepción de la última. Esto es porque solo al final del plazo de endeudamiento se devuelve el principal. En todos los demás períodos solo se van pagando los intereses acumulados.
Continuando con los datos del ejemplo anterior, con el método inglés tendríamos el siguiente cronograma de pagos:
| Intereses | Cuota | Principal | Saldo | |
|---|---|---|---|---|
| 0 | 15.000,00 | |||
| 1 | 450,00 | 450,00 | 15.000,00 | |
| 2 | 450,00 | 450,00 | 15.000,00 | |
| 3 | 450,00 | 450,00 | 15.000,00 | |
| 4 | 450,00 | 450,00 | 15.000,00 | |
| 5 | 450,00 | 450,00 | 15.000,00 | |
| 6 | 450,00 | 15.000,00 | 15.450,00 | – |
| suma | 2.700,00 | 15.000,00 | 17.700,00 |
