Sistema de amortización alemán

Esta forma de amortización de préstamos tiene dos vertientes. En una de ellas se equipara al sistema italiano, de cuotas de amortización de capital (A) constantes. En la otra, el término amortizativo (a) es constante, siendo una modalidad del método francés.

Desde Economipedia hemos optado por la segunda, ya que es la que se enseña en la mayoría de los planes de estudios universitarios. Sin embargo, es muy habitual encontrar la primera opción (italiano) si se realiza una búsqueda en Internet.

Así, en esta opción la diferencia entre ambos se debe al momento del pago de intereses, por anticipado en el alemán y al final del período en el francés. Este método es, después del sistema francés, el más utilizado en hipotecas.

Se pueden efectuar dos transformaciones para asemejarlo al sistema de amortización francés (ver imagen). La primera es para convertir el interés anticipado en uno vencido (francés) y la segunda es para transformar el capital inicial en uno equivalente pospagable.

• i*: tipo de interés anticipado
• i: tipo de interés vencido (francés)
• Co: capital prestado
• Co´: capital transformado por el cambio de tipo de interés

En primer lugar, a partir de las transformaciones de antes, calculamos el término amortizativo constante (a) de forma similar a como hacíamos en el método francés. Empleamos la primera fórmula despejando de ella dicho término (a) en la segunda.

• a: término amortizativo constante
• Co´: capital prestado transformado
• i: tipo de interés anual vencido (transformado)
• n: número de períodos

Una vez calculada la cuota, también interesa conocer la cuota de capital amortizado (Ak o An), el montante de interés (Ik), el capital amortizado acumulado (mk) y el capital vivo (Ck), todos ellos en cada período.

Para el cálculo de dichos componentes utilizamos los intereses anticipados (i*) y el capital original prestado (Co). Es decir, no los transformamos, ya que no es necesario y las fórmulas en este caso son sencillas de aplicar.

No olvidemos que en este caso el interés (Ik) se calcula siempre sobre el capital vivo a principios de año (Ck-1) y que hay que pagar una cuota (Io) al principio, calculada sobre todo el préstamo concedido (Co). Al final de la vida del préstamo no se pagan intereses, solo capital (An), coincidiendo esta última cuota de capital con el término amortizativo constante (a).

• Ak y An: Cuotas de amortización de capital año k y año n (último)
• Co: Capital prestado
• Ik: cuota de interés periódica en k
• Ck y Ck-1: capital en el período k y k-1
• i*: tipo de interés anticipado del préstamo
• n y k: número de períodos total (n) y hasta la fecha (k)
• mk: Capital amortizado en k

Imaginemos un préstamo de 10.000 €, al 3% y a 5 años. En el momento de la concesión tendremos que pagar los intereses (anticipados) calculados sobre el capital concedido. A partir de aquí, funciona de forma similar al método francés.

Comenzamos obteniendo el término amortizativo constante (a) teniendo en cuenta las transformaciones explicadas. De esta manera, en este primer cálculo usamos i y Co´, es decir, el capital prestado transformado y el interés vencido.

Para calcular Ak es importante observar que la cuota de amortización de capital del último año (An) coincide con el término amortizativo (a), ya que no hay intereses (anticipados). Por tanto, An sería el importe de a.

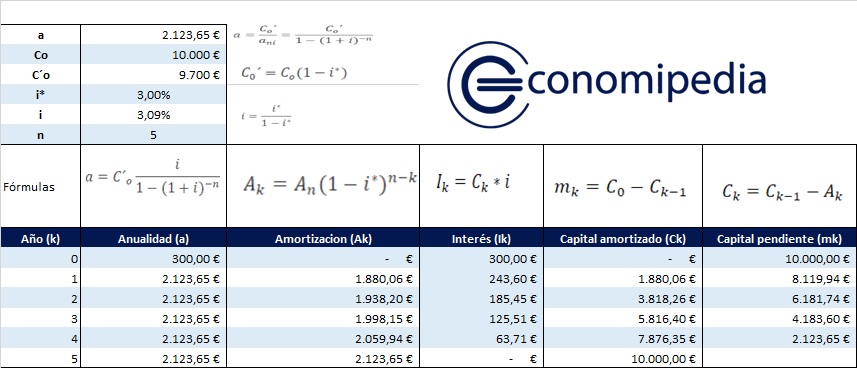
Podemos observar que en el sistema de amortización alemán la cuota (a) es constante, como en el francés. Por otro lado, los intereses disminuyen cada año y se pagan por anticipado, de manera que en el año 0 pagamos el primero (300 €) y en el año n no pagamos ninguno.

En en el sistema de amortización alemán la cuota (a) no es constante. Es el capital o llamado tambien amortización la cual es constante. Para hallar la amortización constante solo es dividir el monto del préstamo entre el número de periodos pactados. Saludos.

No puedes estar más equivocado. Lo estás confundiendo con el sistema con cuotas de amortización constantes.

Buenas tardes, cual es la diferencia entre la amortización italiana y la amortización alemán??? Si a lo que tengo entendido que en la amortización Alemán el capital amortizable es contante y en la amortización italiana la amortización es contante, me podrían ayudar por favor….
Saludos desde Bolivia

Hola Brenda

El problema viene porque como comentamos en el artículo, hay dos vertientes. La académica considera el método alemán como una variante del francés, de manera que los terminos amortizativos (a) son constantes. Ten en cuenta que estos términos son la suma de las cuotas de capital (Ak) y de intereses (Ik).

La otra es la que lo asemeja al método italiano, en cuyo caso las cuotas de capital (A) son constantes, de ahí que no lleven el subíndice. Esta variante se puede comprobar haciendo una búsqueda en Google. Nosotros hemos optado por la académica, al ser la que se suele estudiar en la asignatura de matemáticas financieras en la universidad.

De esta forma, resumiendo, será una variante del francés, con intereses anticipados y término amortizativo (a) constante.

Gracias por venir a Economipedia.

Hola Luís Arturo

La verdad es que existen dos variantes. la que mostramos nosotros, que es la que suele estudiarse en los planes de estudio universitarios. En ella es una variante del método francés, con intereses anticipados y términos amortizativos constantes (a).

La que mencionas, con cuotas de capital (A) constantes, sería (desde un punto de vista académico) el método de cuotas constantes o italiano. Te dejamos el enlace por si quisieras revisarlo.

https://economipedia.com/definiciones/sistema-de-amortizacion-italiano.html

Gracias por venir a Economipedia

QUE SE RECOMIENDA A LA HORA DE TOMAR UN PRESTAMOS EL SISTEMA ALEMAN O EL SISTEMA FRANCES.
ENTIENDO EL CALCULO DE AMBOS NO INSIDE EN Q SEA VARIABLE EN CADA CUOTA OSEA UNA VEZ Q LO TOMASTE EL PLANDE CUOTAS OBTENIDO NO SE MODIFICA MAS. ENTIENDO Q CON EL SISTEMA INFLACIONARIO Q HAY EN ARGENTINA POR EJE CONVIENE HOY POR HOY TOMAR UN PRESTAMO CON SISTMA ALEMAN . ESTOY EN LO CORRECTO?
GRACIAS SI ME ACLARAN TODO ESTO

Hola Diego;

Muchas gracias por tu pregunta.

Como dice la definición, ambos sistemas presentan muchas similitudes entre sí. Es decir, son sistemas muy parecidos.

No obstante, el sistema de amortización, casi siempre, viene determinado por el banco. En este sentido, el escogido por estos es el sistema de amortización francés. Las similitudes entre ambos sistemas hace que no se cuestiona la eficiencia del sistema de amortización francés, así como la hipótesis de que dicho sistema es el mejor para ser usado por la banca.

Espero haberte ayudado.

Un saludo de parte del equipo de Economipedia 🙂

¿¿cómo se obtuvo la amortización Ak de 1880.06 si Ik es 300 y no puedes obtener el 243 sin tener antes el Ck que no puedes obtener sin tener antes el Ak??
ayuda por favor

Hola Leslie
El problema que diferencia al sistema alemán del francés (es una variante de este) es que los intereses son anticipados. Esto quiere decir que el interés del momento de concesión (momento cero) sería Io=Co*i=300. Después, en el año uno, en el francés el I1 sería I1=Co*i=10.000*0.03=300, pero en el alemán, al ser los intereses anticipados sería I1=C1*i=8119.94*0.03=245.60. Es decir, utilizamos el capital vivo (C1) del mismo año y no del año anterior (Co). Una vez tenemos Ik, Ak se obtiene mediante la fórmula a-Ik. Como a es constante sería A1=a-I1=2123.65-243.60=1880.06 y así sucesivamente.
Te dejamos el enlace al método francés:
https://economipedia.com/definiciones/sistema-de-amortizacion-frances.html
Esperamos haberte resuelto la duda y gracias por venir a Economipedia.

Buenas, mi duda es como se calculo el saldo 8119.94?. Entiendo que seria la cuota constante menos el interés. Pero a su vez , el interés para calcularlo depende del saldo pendiente, en este caso 8119.94. Es mi gran confusión

Hola Sonia, hemos revisado la definición y hemos simplificado los diferentes cálculos para asemejarlo al sistema de amortización francés, ya que de hecho es una modalidad de este. Verás ahora que el ejemplo es mucho más sencillo de entender y calcular gracias a las dos transformaciones iniciales del capital prestado (Co a Co´) y del interés anticipado a vencido (i* a i).
Si te parece vuelve a revisar el ejemplo y si necesitas alguna aclaración adicional no dudes en preguntar.
Gracias por venir a Economipedia y por la aportación.

Hola de nuevo Leslie
Hemos revisado la definición y hemos simplificado los diferentes cálculos para asemejarlo al sistema de amortización francés, ya que de hecho es una modalidad de este. Verás ahora que el ejemplo es mucho más sencillo de entender y calcular gracias a las dos transformaciones iniciales del capital prestado (Co a Co´) y del interés anticipado a vencido (i* a i).
Si te parece vuelve a revisar el ejemplo y si necesitas alguna aclaración adicional no dudes en preguntar.
Gracias por venir a Economipedia y por la aportación.

y cómo se obtiene el 8119.94, sin tener el 1880, que a su vez no se puede obtener sin el 243.60, que a su vez no se obtiene sin el 8119………

Hola Noe, hemos revisado la definición y hemos simplificado los diferentes cálculos para asemejarlo al sistema de amortización francés, ya que de hecho es una modalidad de este. Verás ahora que el ejemplo es mucho más sencillo de entender y calcular gracias a las dos transformaciones iniciales del capital prestado (Co a Co´) y del interés anticipado a vencido (i* a i).
Si te parece vuelve a revisar el ejemplo y si necesitas alguna aclaración adicional no dudes en preguntar.
Gracias por venir a Economipedia y por la aportación.

Buenas tardes. En el Bco me ofrecen un préstamo al 35% anual con un sistema Alemán a 60 meses. Cuando les dije que prefería sistema Francés, me dijeron que solo prestaban con el Alemán. Que es lo que hace que tomen ese sistema y no el Francés?.
Gracias

Hola Juanf
La verdad es que como el sistema alemán es una variante del francés en que los intereses se pagan por anticipado, lo que sucede es que al cambiar el tipo de interés prepagable a uno pospagable, este suele ser algo mayor, quizá ese sea el motivo.
Aun así pregunte y si no le convence reclame o si lo ve oportuno, cambie de entidad.
Gracias por venir a Economipedia.

Hola! Disculpa como hiciste para hacer el cálculo de C1, cómo hacemos para conocer la variante? Ya que para aplicar la fórmula no tenemos todos los datos.
Gracias

Hola Juan León, hemos revisado la definición y hemos simplificado los diferentes cálculos para asemejarlo al sistema de amortización francés, ya que de hecho es una modalidad de este. Verás ahora que el ejemplo es mucho más sencillo de entender y calcular gracias a las dos transformaciones iniciales del capital prestado (Co a Co´) y del interés anticipado a vencido (i* a i).
Si te parece vuelve a revisar el ejemplo y si necesitas alguna aclaración adicional no dudes en preguntar.
Gracias por venir a Economipedia y por la aportación.

EN QUE PAISES , SE USA ESTE METODO DE AMORTIZACION ALEMAN? PORQ TENGO ENTENDIDO QUE EL MAS COMUN ES EL SISTEMA DE AMORTIZACION FRANCES
EN ALEMANIA ES COMUN UTILIZAR ESTE TIPO DE AMORTIZACION ALEMAN EN SU ECONOMIA?

Hola Mariela
La verdad es que el método alemán no suele utilizarse, siendo el preferido de los bancos en la mayoría de países el francés. De hecho es el habitual en las hipotecas. Aun así, un lector nos comentó que su banco le había ofrecido los dos, aunque esto es muy poco frecuente.
Gracias por venir a Economipedia.

que paises en la actualidad estan utilizando el sistema de amortizacion aleman

Hola Iván
El método alemán es poco frecuente, en la mayoría de países se usa el francés. De hecho, es el habitual en las hipotecas.
Gracias por venir a Economipedia

que paises utilizan el metodo de amortizacion aleman?

Hola Andrés
El habitual en la mayoría de países es el francés, aunque un lector nos comentó que su banco le había ofrecido los dos, esto es muy infrecuente.
Gracias por venir a Economipedia

BUENOS DIAS
UNA CONSULTA QUE PAISES UTILIZAN EL SISTEMA ALEMAN..?

Hola Dafnne
Nos han preguntado esto mismo varios lectores. El habitual es el francés, aunque algún lector nos comentó que su banco le había ofrecido los dos. Las hipotecas suelen amortizarse, en la mayoría de países, con el método francés.
Gracias por venir a Economipedia.

En q países se usa el Sistema de amortización alemán

Hola Madelin
Nos han hecho esta misma pregunta varios lectores. El método más frecuente es el francés, de hecho, el método alemán no es habitual en la mayoría de países. Enre otras cosas, por la comodidad de cálculo del primero.
Gracias por venir a Economipedia.

Es recomendable el método Americano para una hipoteca.

Hola Dinora,

Muchas gracias por tu pregunta. Te dejo por aquí el enlace a nuestro artículo del sistema de amortización americano. Te recomiendo que en base a tus circunstancias, compares cuál de los modelos es más beneficioso.

https://economipedia.com/definiciones/sistema-de-amortizacion-americano.html

Espero haberte ayudado.

Un saludo de parte de todo el equipo de Economipedia 🙂