Análisis discriminante

Por tanto, estamos ante un tipo de procedimiento estadístico que lo que busca es agrupar en función de ciertas semejanzas. De esta forma, permite cuantificar la probabilidad de pertenecer a uno u otro grupo. Estos grupos son conocidos a priori, a diferencia del análisis clúster.

Vamos a ver cómo sería el modelo matemático de un análisis discriminante.

Es muy sencillo, ya que se basa en un sistema de ecuaciones lineales. Por supuesto, el análisis se complica más, pero esto quedaría fuera de la labor de Economipedia, la economía sencilla.

Como vemos, son un conjunto de ecuaciones cuya variable dependiente (y) representa unas puntuaciones determinadas. Estas, a su vez, son funciones lineales de otras variables discriminantes (X) y de una serie de parámetros (a).

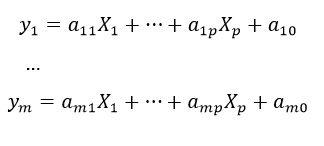
El objetivo, a través de estas combinaciones lineales, es maximizar la varianza entre grupos y minimizar la que se da inter grupos. De esta forma, se pueden agrupar los nuevos casos con cierta probabilidad de la que podemos conocer su valor, siempre que cumplan estos criterios.

Veamos como se puede llevar a cabo un análisis de este tipo:

1. En primer lugar hay que crear una tabla de datos con casos y variables. También se incluye una variable categórica que define cada uno de los grupos.
2. A continuación, se genera el modelo matemático con datos numéricos. Este estará basado en el que vimos en el apartado anterior. Softwares estadísticos como SPSS o el gratuito R automatizan todo el proceso.
3. Por último, con este análisis podremos explicar por qué cada caso pertenece a uno u otro grupo y, además, establecer un criterio de pertenencia para los casos nuevos. Este estará basado en la probabilidad de englobarse dentro de uno u otro.

Para terminar, veamos algunos ejemplos de aplicación del análisis discriminante.

Recordemos, además, que en todos ellos el objetivo es crear una función discriminante que agrupe cada nuevo caso según una probabilidad.

• Queremos clasificar diversos países en función de sus datos macroeconómicos: Países subdesarrollados, emergentes o desarrollados (grupos). Creamos la función discriminante de manera que podamos calcular la probabilidad de un país de pertenecer a uno u otro grupo.
• Queremos realizar una campaña de marketing y nos interesa saber en qué grupos clasificar a los individuos: Así, podremos responder a ciertas preguntas como cuáles serían las características de un cliente ocasional.
• Queremos conocer el nivel de riesgo (grupo) de determinados clientes respecto a la concesión de un crédito: Utilizaremos variables relativas a su renta, gastos mensuales, historial o tipo de trabajo. La función discriminante nos aporta información relevante sobre la solvencia.

Como vemos, el análisis discriminante es muy útil en muchas situaciones. Pero no solo relacionadas con la economía, también se utiliza en medicina, geología o biología, entre otros campos.