Variable matemática
Una variable matemática es un símbolo utilizado para proponer fórmulas, algoritmos o ecuaciones. Esta, a su vez, puede tomar diferentes valores, dependiendo estos de otras variables, así como de una serie de parámetros y de ciertas constantes.
Por tanto, son de inestimable ayuda para plantear problemas o modelos matemáticos. De hecho, sin ellas no se podrían resolver muchos problemas complejos.
No debemos confundirlas con el concepto de incógnita, que es algo desconocido. Pues la variable se caracteriza por que toma un valor indeterminado, pero que se puede calcular.
Diferencia entre constante y variable matemática
En muchas ecuaciones, veremos una serie de números, o letras minúsculas (que suelen ser vocales). Estas son las constantes. La diferencia con las variables es que las primeras son valores fijos, mientras que las segundas toman valores diferentes; de ahí su nombre. Por tanto, esta última varía en función de esa constante y otras variables.
La constante tiene dos significados básicos. Por un lado, puede indicarnos el valor que toma la variable dependiente cuando las independientes son cero. Por otro, relacionado con el anterior, puede indicarnos el punto de corte de la función en un eje de coordenadas. Esto lo veremos con más detalle en el ejemplo.
Variable dependiente e independiente
Las variables matemáticas suelen representarse por X, Y o Z y van acompañadas de números u otras letras, a los que llamaremos parámetros. Cuando hay un número elevado de variable se suelen utilizar subíndices en la nomenclatura. De esta forma, se utiliza solo una letra con una numeración.
Las variables pueden ser independientes o dependientes. Las primeras toman valores a los que llamamos exógenos, mientras que en las segundas los denominamos endógenos. Es decir, las primeras son explicativas de las segundas. De esta forma, dando valores a una podemos obtener los de la otra.
Así, las independientes tienen un número o parámetro que las acompaña. Indica como varía la dependiente en función de estas. El valor absoluto informa sobre el tamaño de dicha variación, mientras el signo aclara si esta es directa (en la misma dirección) o inversa (en dirección contraria).
Ejemplo de variable matemática: la ecuación de la recta
A continuación, vamos a utilizar un ejemplo de una de las ecuaciones matemáticas más conocidas, la de la recta.
En ella tenemos una variable independiente o X, que se relaciona con el eje de ordenadas. Así como otra dependiente o Y, que se sitúa en el eje de abscisas.
Veamos la imagen y después la comentamos:
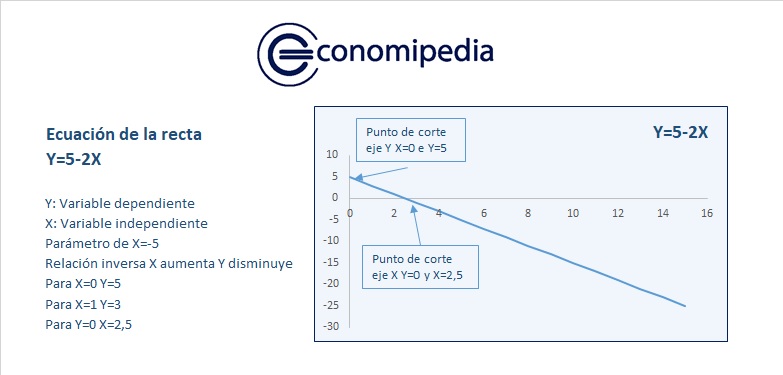
Como vemos en la imagen, podemos observar una ecuación de la recta.
Si queremos utilizar un formato genérico, sería Y = a+bX.
De esta forma, el parámetro es b o (-2) en el ejemplo, mientras que la constante es a o 5. El punto de corte de los ejes se calcula igualando X e Y a cero y calculando la otra variable matemática.
