Historia de la geometría: antecedentes y desarrollo desde su origen
La historia de la geometría comienza con las primeras civilizaciones que hacían uso de esta rama de las matemáticas de una forma práctica, específicamente los pueblos del valle del Indo y de Babilonia que conocían los triángulos obtusos, alrededor del 3000 a.C.
En los escritos del escriba egipcio Ahmes (1550 a.C.) se utilizan métodos para calcular el área de un círculo. Por su parte, los babilonios tuvieron reglas generales para medir volúmenes y áreas.

Ambas civilizaciones, los egipcios y babilonios, conocían versiones del teorema de Pitágoras 1500 años antes de las versiones de los pitagóricos. Por otra parte, los indios del periodo védico (1500-100 a.C.) utilizaban la geometría en la construcción de altares.
Índice del artículo
- 1 Antigua Grecia
- 2 Influencia islámica
- 3 Desarrollo del legado europeo
- 4 Paso a la modernidad
- 5 La geometría no euclidiana
- 6 Referencias
Los griegos estuvieron inclinados hacia el desarrollo de la matemática durante mucho tiempo. Personajes como Pitágoras y Platón, relacionaban a los números con todo lo que existe en el mundo. Para ellos la matemática era la llave para interpretar el universo; este ideal siguió en los seguidores de pitagóricos durante varios siglos.
Tales de Mileto fue de los primeros griegos en contribuir a los avances de la geometría. Pasó mucho tiempo en Egipto y de estos aprendió los conocimientos básicos. Fue el primero en establecer fórmulas de medición de la geometría.

Consiguió medir la altura de las pirámides de Egipto, midiendo su sombra en el momento exacto en el que su altura era igual a la medida de su sombra.

Dentro del aporte más significativo de Pitágoras (569 a.C. – 475 a.C.) a la geometría se encuentra el famoso teorema de Pitágoras, que establece que dentro de un triángulo rectángulo el cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los lados restantes.
El trabajo más destacado que se ha podido rescatar desde la antigüedad ha sido el estudio Los Elementos, de Euclides de Alejandría (325 a.C. – 265 a.C.), realizado durante los años 300 a.C. Es una obra de gran valor histórico que ha servido como base para la enseñanza de la matemática por más de 2000 años.

Los Elementos fue uno de los primeros libros y recopilaciones de estudios que explicaban principios matemáticos que podían ser aplicados a cualquier situación. Incluye los postulados, que son los principios fundamentales de la geometría en su trabajo. Por otro lado, se encuentran los principios cuantitativos conocidos como las nociones básicas.
La enseñanza de Euclides redujo los instrumentos de construcción dentro de la geometría a solo dos: una regla sin medidas y una brújula. Esto generó los tres problemas clásicos que no hallaron respuestas hasta el siglo XIX: la cuadratura del círculo, la duplicación del cubo y la trisección de un ángulo.
Para los antiguos, los dos entes geométricos ideales eran la línea recta y el círculo, por lo que la mayoría de los teoremas geométricos que se proponían eran producto de la exploración con estos instrumentos.
La geometría también fue de provecho para los griegos en cuanto al estudio de los astros. Realizaron el cálculo de los movimientos a través de la observación e hicieron planos geométricos del cielo estableciendo a la Tierra como un punto central, y tanto al Sol como la Luna y los otros planetas como entes que se movían a su alrededor, rotando en un conjunto de círculos.
Uno de los aportes más influyentes fue el Almagesto, escrito en el siglo II d.C por Claudio Ptolomeo (100 d. C.- 170 d.C), un tratado astronómico contenedor del catálogo de las estrellas. Fue el texto más completo de su época e influyó en los estudios astronómicos de forma trascendental hasta muy avanzada la Edad Media. Formó parte de los medios que más popularizó el sistema geocéntrico, que afirmaba que la Tierra era el centro del universo.

Hacia los siglos IX, cuando el mundo árabe estaba en su gran expansión, mucha de su cultura impregnó varias áreas de la ciencia y las artes. Eran grandes admiradores de los trabajos matemáticos y filosóficos de los griegos.
Una de las ramas más exploradas dentro de sus necesidades fue la astronomía, con el fin de ubicar la orientación exacta en la que se encontraba la Meca para poder realizar las oraciones.
Siguiendo los estudios de Euclides y otros aportes como los de Ptolomeo, los musulmanes desarrollaron la proyección estereográfica, es decir la proyección de la esfera celeste en el plano para utilizarla como mapa. Esto significó progresos en cuanto al estudio de la trigonometría.
Dentro de los personajes más representativos se encuentra Thābit ibn Qurra (826/36-901) quien realizó traducciones relevantes de los textos antiguos de Apolonio, Arquímedes, Euclides y Ptolomeo. Algunos de estos son las únicas versiones sobrevivientes de las escrituras antiguas.
Las exploraciones en cuanto a la geometría astronómica también permitieron la creación de uno de los instrumentos más representativos, el astrolabio, con lo que simplificaron los cálculos astronómicos del momento. Además este instrumento también les permitía conocer el tiempo y finalmente conseguir la orientación a la Meca.
En el siglo XII, tras la inserción de las enseñanzas clásicas de los griegos gracias a la expansión musulmana y el desarrollo de sus mismos descubrimientos, se comenzaron a realizar traducciones de los textos al latín directamente desde el griego o a partir del idioma árabe.
Esto abriría paso a un nuevo aprendizaje dentro de Europa que se vería impulsado por el Renacimiento. Comenzó el redescubrimiento de nociones como las “pruebas”, un concepto desarrollado entre los griegos que se interesaba por la demostración de los postulados en la realidad.
El conocimiento también se reflejó en las artes, como la pintura o la arquitectura, ya que la geometría comenzaría a ser parte fundamental para el desarrollo de la perspectiva en el arte.
Filippo Brunelleschi (1377–1446), fue quien logró desarrollar la perspectiva lineal a través de la matemática. El objetivo de esta teoría era lograr representar en un plano un espacio tridimensional a partir de cómo era percibido por el ojo humano. Así establece que todas las líneas en un cuadro debían converger o encontrarse en un punto de fuga para poder generar la sensación de profundidad.

Brunelleschi fue el primero en describir la perspectiva como un procedimiento científico y esto funcionó como las bases de trabajos posteriores dentro de las artes.
Dentro de otros ejemplos de la aplicación de la geometría al estudio del arte y del ser humano en sí mismo, se encuentra el trabajo de Leonardo da Vinci (1452-1519) en su dibujo El Hombre Vitruvio. Se trata de un estudio basado en las proporciones más perfectas para el cuerpo humano mediante un análisis geométrico de su estructura.

Entre otros ámbitos también destaca la arquitectura, donde diversos elementos como la simetría y el balance comenzaron a figurar como características fundamentales. Puertas y ventanas cuadradas, rectangulares, posicionadas de una forma equilibrada; utilización de elementos clásicos de la antigüedad como columnas, cúpulas y bóvedas.
El análisis de las perspectivas y las proyecciones durante el Renacimiento fue uno de los incentivos para despertar el interés de los matemáticos. A partir de este momento comienzan a fundarse bases matemáticas más sólidas y complejas dentro de la geometría.
Uno de los trabajos más importantes para la modernidad fue el del arquitecto Girard Desargues (1591–1661), que supusieron el inicio para la geometría proyectiva. Por una parte estableció que las líneas paralelas en una proyección debían converger en un punto de la línea del infinito, es decir, el horizonte.
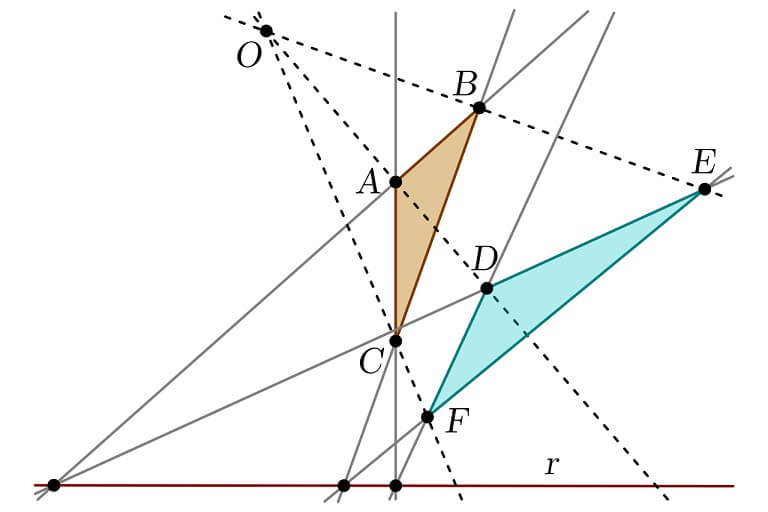
Por otro lado, también descubrió lo que sería reconocido como el teorema de Desargues, que establece la relación entre dos figuras que pueden considerarse “proyectivas”. Además se encargó de simplificar los trabajos de Apolonio con respecto a las secciones de un cono, realizando analogías entre esta figura y el cilindro.
Otro gran suceso del período fue la creación de la geometría analítica mediante los estudios de René Descartes (1596-1650) y Pierre de Fermat (1601-1665) de forma independiente. Se trata del estudio de la geometría a través del uso de un sistema de coordenadas.

Hacia los siglos XVIII y XIX se iniciaron estudios que derivaron en la geometría no euclidiana. Específicamente fueron Gauss, Johann Bolyai y Lobachevsky, quienes comprobaron que el quinto postulado de Euclides, conocido como postulado paralelo, no podía comprobarse.
De esta forma desarrollaron un tipo de geometría en la que este postulado fuese calificado como falso. Esta nueva forma fue exitosa al dar resultados satisfactorios en estilos de geometría que no necesariamente cumplían con todos los postulados de Euclides. Así nacieron posteriormente la geometría hiperbólica y la geometría elíptica.
Cabe resaltar el trabajo de Leonhard Euler (1707-1783) en el siglo XVIII, con respecto al desarrollo de la notación matemática. Posteriormente, el siglo XX traería consigo el desarrollo de campos más específicos de la geometría entre los cuales se encuentran:
–La geometría algebraica: es una rama de la matemática que combina el álgebra abstracta y la geometría analítica.
–La geometría finita: se trata de un sistema geométrico que está conformado por una cantidad finita de puntos, es decir, que tienen fin o límite y por ende, pueden ser medidos.
–La geometría digital: es una rama de la informática que realiza el estudio de algoritmos y estructuras de datos que pueden representarse en términos geométricos.
- (2016) Qué convirtió a los Elementos de Euclides en el único libro que puede competir con la Biblia. BBC. Recuperado de bbc.com
- Los tres problemas clásicos de la matemática griega. Universidad de Antioquia. Recuperado de docencia.udea.edu.co
- Heilbron J.L (2020). Geometry. Encyclopædia Britannica. Recuperado de britannica.com
- History of geometry. Wikipedia, the free encyclopedia. Recuperado de en.wikipedia.org
- Analytic geometry. Wikipedia, the free encyclopedia. Recuperado de en.wikipedia.org
- (2017) Geometry And Mathematics In The Renaissance. Recuperado de ukessays.com
- Sáiz A. Perspectiva Lineal en Brunelleschi. Universidad de Valencia. Recuperado de uv.es
- The Editors of Encyclopaedia Britannica (2019). Renaissance architecture. Encyclopædia Britannica. Recuperado de britannica.com
- Andersen K (2020). Girard Desargues. Encyclopædia Britannica. Recuperado de britannica.com
- (2011) Una Interesante Introducción a la geometría computacional. Recuperado de gaussianos.com
